Поступат.: скорости всех его точек одинаковы и равны скорости центра масс ТТ: 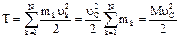 .
.
Вращат.: скорость произвольной точки ТТ равна: 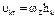 , где
, где 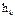 - расстояние от точки до оси Оz.
- расстояние от точки до оси Оz. 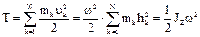 , где
, где
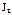 - момент инерции тела относит. оси вращения Оz.
- момент инерции тела относит. оси вращения Оz.
Плоск.: рассм. такое движение, как совокуп. поступат. движения тела вместе с центром масс С и вращат. вокруг подвижной оси Сz, движущейся поступат. вместе с центром масс. Относит. скорость точки тела равна: 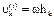 . Подставив эту скорость в формулу Кенига:
. Подставив эту скорость в формулу Кенига: 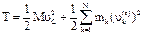 , получим:
, получим: 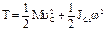 .
.
 2015-05-06
2015-05-06 542
542








