Сформулировать и доказать теорему о кинетической энергии механической системы различных формах

Система N материальных точек. Масса k-ой точки - 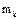. К каждой k-ой точке системы (k = 1, 2,..., N) прилож. равнодействующие внешних 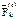и внутренних 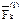сил.

ДУ движения: 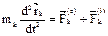или 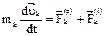(1). Т.к. масса постоянна внесём ее под знак производной и умножим (1) скалярно на 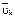: 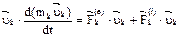(2). Внося 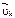под знак производной, суммируем (2) по k и поменяем знаки суммир. и дифференцир. местам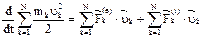и: или 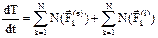(2): производная по времени от кинетической энергии системы равна сумме мощностей всех действующих на систему внешних и внутренних сил.

Умножим (2) слева и справа на dt и учтём, что 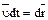: 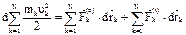или 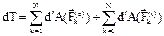(3): дифференциал кинетической энергии механической системы равен сумме элементарных работ всех действующих на систему внешних и внутренних сил.

Проинтегрируем обе части (3) от нач. положения системы до конеч., изменяя порядок суммир. и интегрир.: 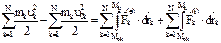или 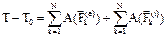: изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме полных работ всех действующих на систему внешних и внутренних сил на соответствующем перемещении.