Работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинения (или сжатия) пружины

Работа не зависит от вида деформации (сжатие или растяжение).

г) Работа силы тяжести:

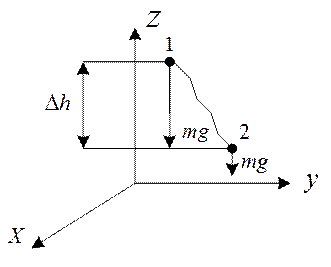
Рис. 37

Пусть точка перемещается из положения 1 в положение 2.

По определению работы:

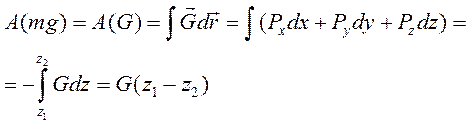(147)

Работа силы тяжести:

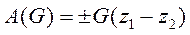(148)

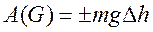(149)

Работа положительная, если 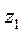> 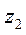, т.е. начальная высота точки приложения силы выше, чем в конечный момент, т.е. происходит движение в сторону силы.

Работа отрицательная, если 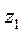< 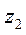, т.е. начальное положение точки приложения силы тяжести ниже конечного, т.е. происходит движение противоположно направлению действия силы.

Работа равна нулю, если в начальный момент и в конечный момент времени точка приложения силы тяжести находится на одинаковой высоте.

д) Работа силы трения скольжения:

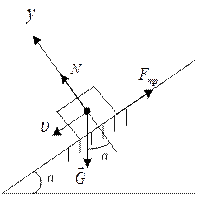
Рис. 38

Запишем второй закон Ньютона в проекции на ось Y:

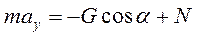(150)

Движение вдоль оси У отсутствует, поэтому а_у = 0, т.е.

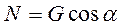(151)

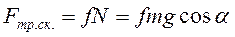(152)

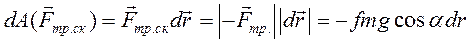(153)

е) Мощность силы.

Средней мощностью силы называется отношение работы этой силы к тому промежутку времени, за которое она совершена:

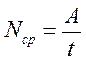(154)

Мгновенной мощностью силы называется первая производная по времени от работы этой силы:

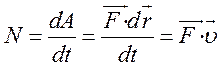(155)

То есть, мощность определяется скалярным произведением силы на скорость точки приложения этой силы.

ж) Элементарная работа момента силы.

Пусть движение по траектории происходит под действием силы 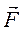, причем 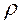- радиус кривизны траектории в точке приложения силы.

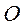- центр кривизны траектории.

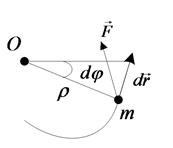
Рис. 39

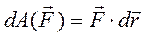(156)

Подставим 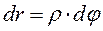в (147), получим элементарную работу момента силы:

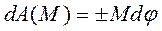(157)

Работа момента силы положительная, если момент направлен в сторону угла поворота.

Работа момента силы отрицательная, если момент направлен против угла поворота.

Работа момента силы равна нулю, если нет угла поворота.

5.3 Теорема об изменении кинетической энергии изменяемых и неизменяемых систем.

а) Дифференциальный вид теоремы:

Запишем второй закон Ньютона для произвольной материальной точки:

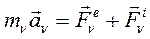(158)

где: 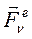- равнодействующая внешних сил приложенных к 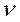- й точке.

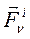- равнодействующая внутренних сил приложенных к 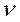- й точке.

Умножим почленно скалярно это уравнение на 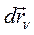, получим:

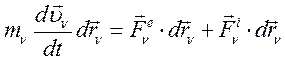(159)

Учтем, что скорость это первая производная от радиус-вектора по времени:

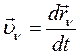(160)

Подставив это выражение (160)в предыдущее равенство (159), получим:

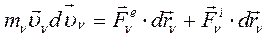(161)

Внесем выражение (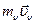) под знак дифференциала, получим:

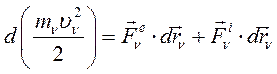(162)

Суммируем по 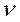, т.е. по всем материальным точкам системы:

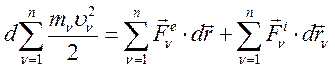(163)

Учтем, что:

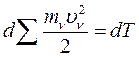(164)

Правая часть выражения (154):

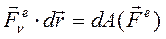(165)

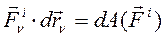(166)

Окончательный вид теоремы об изменении кинетической энергии в дифференциальном виде:

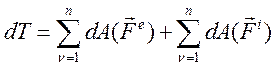(167)

Формулировка: полный дифференциал кинетической энергии механической системы равен алгебраической сумме элементарных работ всех внешних и внутренних сил действующих на систему.

б) Интегральный вид теоремы:

Проинтегрируем выражение, записанное для теоремы об изменении кинетической энергии в дифференциальном виде:

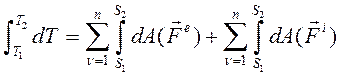(168)

Получим интегральный вид теоремы об изменении кинетической энергии:

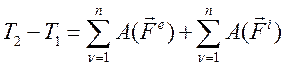(169)

Формулировка: изменение кинетической энергии при перемещении механической системы из одного положения в другое равно алгебраической сумме работ всех внешних и внутренних сил, действующих на систему на этом перемещении.

Это единственная из общих теорем динамики, в которую входят внутренние силы (и то не всегда). Это зависит от того является система изменяемой или неизменяемой.

с) Изменяемые и неизменяемые механические системы.

Определение: изменяемой механической системой называется такая система, у которой расстояние между материальными точками при движении изменяются.