Количество движения механической системы равно произведению массы системы на вектор скорости ее центра масс

Например:

1. Определить количество движения механической системы:

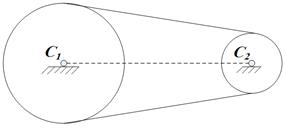
Рис. 27

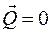, т.к. 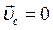(центр масс не движется).

б) Теорема об изменении количества движения (дифференциальный вид).

Выведем ее из теоремы о движении центра масс.

Для ν -той материальной точки по второму закону Ньютона:

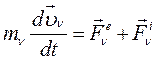(87)

Так как. масса постоянна, то ее можно внести под знак производной. Получим:

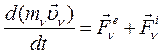(88)

Просуммировав по всем материальным точкам, получим:

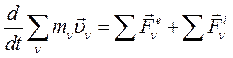(89)

Учтем, что сумма всех внутренних сил механической системы 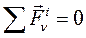- по третьему закону Ньютона.

Получим теорему об изменении количества движения механической системы в дифференциальном виде:

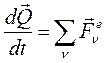(90)

Формулировка: первая производная по времени от количества движения механической системы равна векторной сумме всех внешних сил, действующих на систему, т.е. равна главному вектору всех внешних сил механической системы.

Эти формулы математически показывают, что только внешние силы влияют на движение центра масс и изменение количества движения механической системы, внутренние силы изменить количество движения или движение центра масс не могут.

в) Теорема импульсов (интегральный вид) теоремы об изменении количества движения.

Определение:

1) элементарным импульсом силы называется произведение этой силы на дифференциал времени:

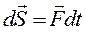(91)

2) импульсом силы за какой-либо промежуток времени называется интеграл вида:

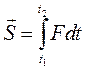(92)

Теорема импульсов: выводится из теоремы об изменении количества движения.

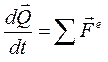(93)

Разделяя переменные, получим:

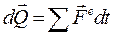(94)

Интегрируем:

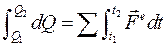(95)

Учитывая, что правая часть уравнения представляет собой сумму импульсов всех внешних сил, получим:

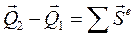(96)

Формулировка: Изменение количества движения за какой – либо промежуток времени равно векторной сумме импульсов всех внешних сил, приложенных к системе в этот промежуток времени.

Эта формулаозначает, что импульс силы и количество движения измеряется в одних и тех же размерностях единиц.

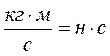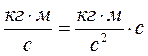; , поэтому количество движения в настоящее время называют импульсом.

г) Закон сохранения количества движения:

1) Если, 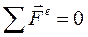, то из теоремы следует, что: , .

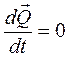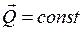Формулировка: если векторная сумма всех внешних сил системы равна нулю, то количество движения системы остается постоянным по величине и направлению.

2) Если, 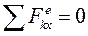, то , .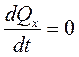

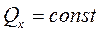Формулировка: если алгебраическая сумма проекций всех внешних сил системы, на какую – либо ось равна нулю, то проекция количества движения на эту ось остается постоянной.

4. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА

Рассматриваемые вопросы:

Общие теоремы динамики механической системы. Теорема об изменении кинетического момента. Момент количества движения материальной точки относительно полюса: алгебраическое значение, направление вектора. Момент количества движения материальной точки относительно оси. Момент количества движения относительно начала координат. Кинетический момент механической системы относительно точки и оси. Кинетический момент вращающегося тела относительно оси вращения. Теорема об изменении кинетического момента. Закон сохранения кинетического момента.

4.1 Момент количества движения материальной точки относительно центра (точки, полюса).

а) Определение: моментом количества движения материальной точки относительно какого-либо центра называется векторное произведение радиус – вектора этой точки на её количества движения.

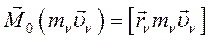(97)

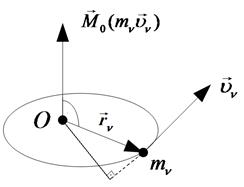
Рис. 28

б) Направление: момент количества движения материальной точки направлен перпендикулярно плоскости траектории движения точки таким образом, чтобы с конца векторного момента можно было видеть направление скорости по отношению к моментной точке против часовой стрелки.

в) Алгебраическое значение момента количества движения точки.

Модуль момента количества движения материальной точки:

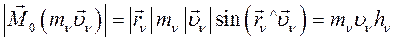(98)

Алгебраическое значение – это произведение количества движения материальной точки на плечо, взятое со знаком плюс или минус.

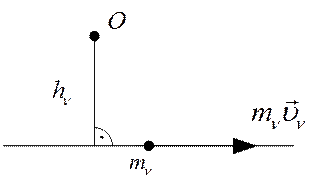
Рис. 2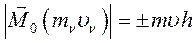9

(99)

Значение момента положительное, если он направлен относительно моментной точки против часовой стрелки.

Значение момента отрицательное, если он направлен относительно моментной точки по часовой стрелке.

Значение момента равно нулю, если моментная точка лежит на линии скорости.

4.2 Момент количества движения относительно оси.

а) Определение: моментом количества движения точки относительно оси называется проекция на эту ось векторного момента количества движения, вычисленного относительно какой – либо точки, лежащей на этой оси.

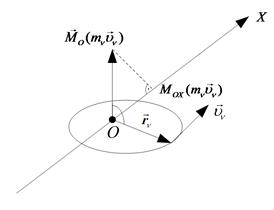
Рис. 30

Алгебраическое значение аналогично:

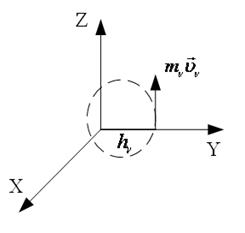
Рис. 31

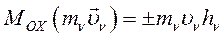(100)

Значение момента количества движения положительное, если он направлен против часовой стрелки, если смотреть с положительного направления оси.

Значение момента количества движения отрицательное, если он направлен по часовой стрелке, если смотреть с положительного направления оси.

Значение момента количества движения равно нулю, если скорость направлена параллельно оси или пересекает эту ось.

Проекции 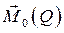на оси координат:

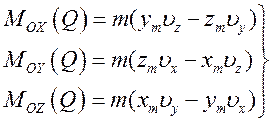(101)

4.3 Кинетический момент механической системы относительно полюса и оси.

а) Кинетический момент механической системы относительно полюса.

Кинетическим моментом механической системы относительно центра (полюса, точки) называется векторная сумма моментов количества движения всех точек системы относительно этого же центра:

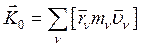(102)

б) Кинетический момент механической системы относительно оси:

Кинетическим моментом механической системы относительно оси называется алгебраическая сумма моментов количества движения всех его точек относительно этой же оси:

Кинетический момент механической системы относительно оси Z:

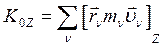(103)

Таким образом - кинетический момент механической системы это главный момент количества движения системы.

4.4 Кинетический момент вращающегося тела относительно оси вращения.

Рассмотрим тело вращения. Рассмотрим движение материальной точки, масса которой m_ν, а линейная скорость .

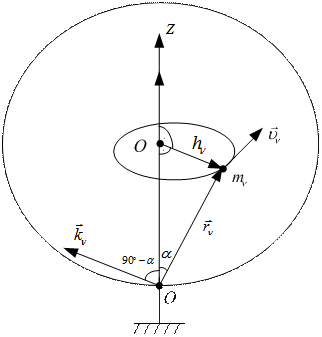
Рис. 32

По определению кинетического момента относительно полюса:

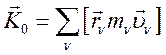(104)

Кинетический момент направлен перпендикулярно радиус-вектору ().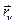

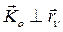Спроектировав кинетический момент 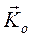на ось 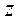, получим:

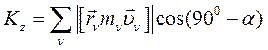(105)

Учитывая, что при вращательном движении линейная скорость определяется по формуле Эйлера, получим:

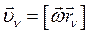(106)

Модуль скорости точки при вращательном движении:

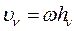(107)

где 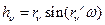, сos (90⁰- 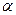) =sin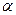

Подставив (98) в формулу (96), получим:

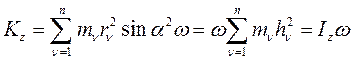(108)

Кинетический момент относительно оси вращения определяется по формуле:

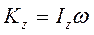(109)

4.5 Вывод теоремы об изменении кинетического момента.

По второму закону Ньютона для ν -той точки:

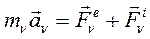(110)

Умножив обе части равенства почленно, векторно на 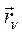, получим:

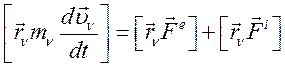(111)

Преобразуем:

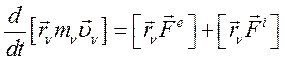(112)

Суммируя по ν т.е. по всем материальным точкам механической системы получим:

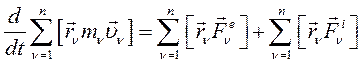(113)

Слева под знаком суммы получаем кинетический момент механической системы относительно полюса О:

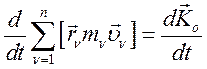(114)

Справа под знаком суммы получаем сумму моментов всех внешних и внутренних сил механической системы относительно полюса О:

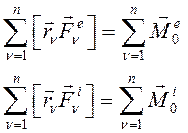(115)

По третьему закону Ньютона сумма моментов всех внутренних сил относительно полюса О равна нулю,

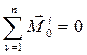(116)

Тогда получим теорему в виде:

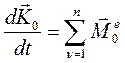(117)

Формулировка: первая производная от кинетического момента по времени, относительно какого – либо центра равна векторной сумме моментов всех внешних сил, действующих на систему относительно этого же центра.

Теорема об изменении кинетического момента относительно оси вращения:

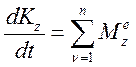(118)

Формулировка: первая производная по времени от кинетического момента, относительно какой – либо оси равна алгебраической сумме моментов всех внешних сил системы относительно этой же оси.

Кинетический момент для твердого тела относительно оси вращения:

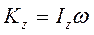(119)

Тогда:

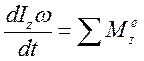(120)

Или:

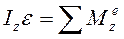(121)

Учитывая, что 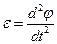получим дифференциальное уравнение вращательного движения твердого тела:

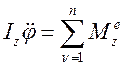(122)

4.6 Закон сохранения кинетического момента.

Следует из теоремы о кинетическом моменте:

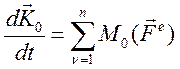(123)

1) Если 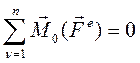, то: 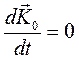, а, следовательно .

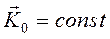Формулировка: если векторная сумма моментов всех внешних сил системы, относительно какого – либо центра равна нулю, то кинетический момент относительно этого центра остается постоянным по величине и направлению.

2) Если 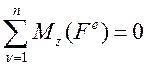, то .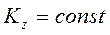

Формулировка: если алгебраическая сумма моментов всех внешних сил системы, относительно какой – либо оси равна нулю, то кинетический момент относительно этой оси остается постоянным.

Например:

При вращении фигуриста на льду все действующие силы параллельны оси Z, а это значит, что кинетический момент относительно оси Z равен нулю.

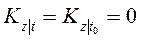(124)

То есть:

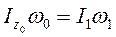(125)

Для увеличения угловой скорости фигурист прижимает руки к туловищу, тем самым уменьшая момент инерции тела относительно оси вращения.

Для уменьшения угловой скорости фигурист расставляет руки в стороны, тем самым увеличивая момент инерции тела относительно оси вращения.

5. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ И