1 Разработать подпрограмму, позволяющую получать последовательности случайных величин 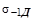 , m,
, m, 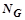 ,
, 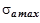 ,
, 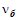 с их законами распределения (принимаем нормальный закон).
с их законами распределения (принимаем нормальный закон).
2 Разработать подпрограмму статистической обработки полученной совокупности случайных чисел 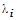 (i =1,2,..., n), где n – число запланированных операций (принять n =100).
(i =1,2,..., n), где n – число запланированных операций (принять n =100).
3 Разработать подпрограмму расчета долговечности L, выраженную наработкой во времени, с использованием формул (6.1)и (5.1).
4 На основании перечисленных подпрограмм разработать программу статистических (имитационных) испытаний (метод Монте-Карло).
5 С использованием разработанной программы выполнить расчет при следующих исходных данных. Предел выносливости детали определить по формулам:
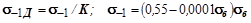 ,
,
где 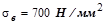 – предел прочности;
– предел прочности;
K =5 – коэффициент снижения предела выносливости с учетом всех факторов.
Показатель наклона кривой усталости детали определить по формуле
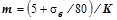 .
.
При расчетах принять: 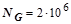 циклов;
циклов; 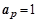 . Значение
. Значение 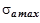 ,
, 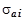 ,
, 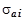 /
/ 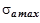 ,
, 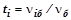 (i =1,2,..., r) принять по результатам обработки осциллограммы случайного процесса (см. лабораторную работу №5). Коэффициенты вариации
(i =1,2,..., r) принять по результатам обработки осциллограммы случайного процесса (см. лабораторную работу №5). Коэффициенты вариации 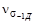 ,
, 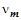 ,
, 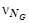 ,
, 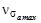 ,
, 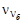 принять равными:
принять равными: 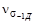 =0,06,
=0,06, 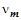 =0,03,
=0,03, 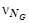 =0.10,
=0.10, 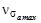 =0,10,
=0,10, 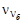 =0,03.
=0,03.
На основании результатов численной реализации программы построить ФРД детали, отложив по оси абсцисс долговечность L (в часах), по оси ординат – вероятность появления трещины P (в процентах). Определить медианный ресурс детали и ресурс, который отвечает вероятности безотказной работы 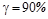 .
.
 2015-05-06
2015-05-06 231
231








