Простейший поток моментов обслуживания

Размеченный граф состояний системы для простейшего потока моментов обслуживания представлен на рис. 14.1 [10].

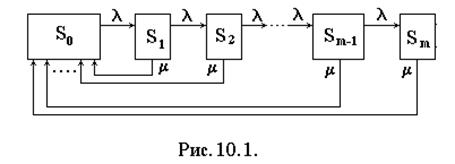
Система уравнений для предельных вероятностей:

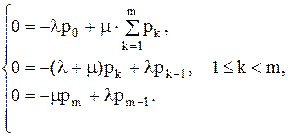
Решение системы можно найти последовательным исключением неизвестных вероятностей. Так как по условию нормировки p₀+p₁+...+p_m=1, то 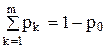. Подставив выражение для суммы в первое уравнение, получим 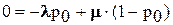. Откуда получим вероятность того, что накопитель свободен

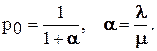
Уравнения при k=1

.

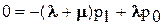Отсюда следует, что

.

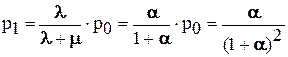Продолжая эту процедуру, находим

.

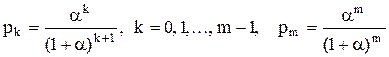Вероятности состояний определяют показатели эффективности системы. Вероятность отказа в обслуживании, т.е. вероятность того, что все места в накопителе окажутся занятыми, равна

.

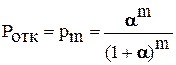Число мест в накопителе, обеспечивающее заданную вероятность отказов,

.

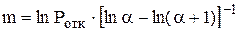Среднее число заявок в накопителе

.

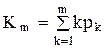Коэффициент загрузки накопителя h=K_m/m.