Первое достаточное условие перегиба

Теорема 9.7. Пусть функция имеет вторую производную в некоторой окрестности точки с и 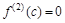. Тогда, если в пределах указанной окрестности вторая производная 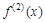имеет разные знаки слева и справа от с, то график этой функции имеет перегиб в точке .

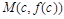Доказательство. Во-первых, имеет касательную в точке 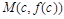, т.к. из условия теоремы вытекает существование конечной производной f’ (c). Далее, из того, что 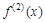слева и справа от с имеет разные знаки, и из Теоремы 9.4 заключаем, что направление выпуклости слева и справа от с является различным.

Теорема доказана.