Второе достаточное условие перегиба

Теорема 9.8. Если функция имеет в точке с конечную третью производную и удовлетворяет в этой точке условиям 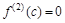, , 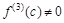то график этой функции имеет перегиб в точке .

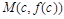Доказательство. Из условия 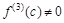и из Теоремы 8.9 ( Теорема 8.9. Если функция f (x) дифференцируема в точке с и 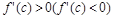, то эта функция возрастает (убывает) в точке с.) вытекает, что 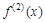либо возрастает, либо убывает в точке с. Так как 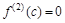, то в обоих случаях найдется такая окрестность точки с, в пределах которой 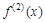имеет разные знаки слева и справа от с. Но тогда по предыдущей теореме график функции имеет перегиб в точке .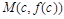

Теорема доказана.