1) Интегралы вида 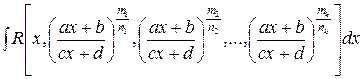 ,
,
где R – рациональная функция своих аргументов; 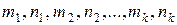 – целые числа;
– целые числа; 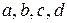 – действительные числа.
– действительные числа.
Такие интегралы вычисляются с помощью подстановки
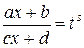 ,
,
где s – общий знаменатель дробей 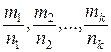 .
.
Пример
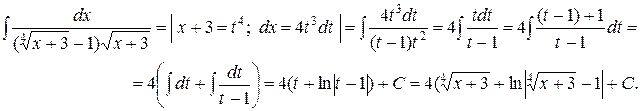
2) Интегралы вида: 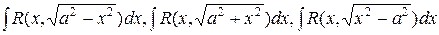 ,
,
где R – рациональная функция своих аргументов.
Такие интегралы вычисляются с помощью соответствующих тригонометрических или гиперболических подстановок:
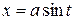 или
или 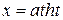 – для интеграла
– для интеграла 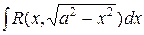 ;
;
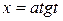 или
или  – для интеграла
– для интеграла 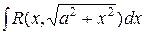 ;
;
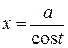 или
или 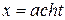 – для интеграла
– для интеграла 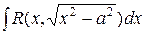 .
.
Пример
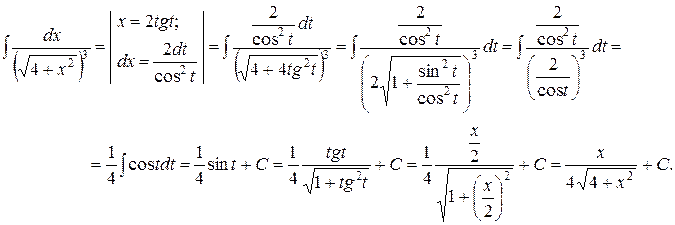 3) Интегралы вида
3) Интегралы вида 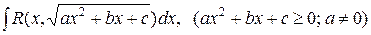 ,
,
где R – рациональная функция своих аргументов.
Такие интегралы вычисляются с помощью выделения полного квадрата в квадратном трехчлене и последующей заменой переменной
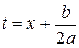 .
.
В результате замены исходный интеграл приводится к одному из интегралов вида 2).
Пример
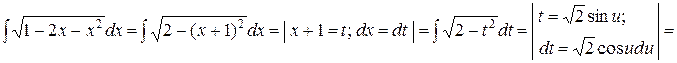
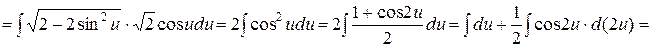
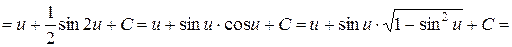
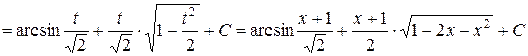 .
.
 2015-04-23
2015-04-23 2238
2238








