2015-04-23
1121
Пусть непрерывная функция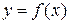 
определена на отрезке 
. Разобьем этот отрезок на n произвольных частей точками
.
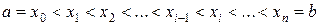В каждом из полученных частичных отрезков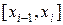 
выберем произвольную точку 
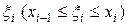. Через 
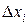обозначим разность 
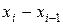, которую условимся называть длиной частичного отрезка .
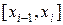Образуем сумму
,
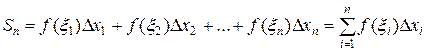которую назовем интегральной суммой для функции 
на отрезке , соответствующей данному разбиению отрезка на частичные отрезки и данному выбору промежуточных точек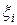 
. Геометрический смысл суммы 
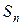очевиден: это сумма площадей прямоугольников с основаниями 
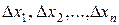и высотами 
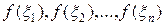(если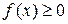 
на отрезке ) (рис. 2.1).
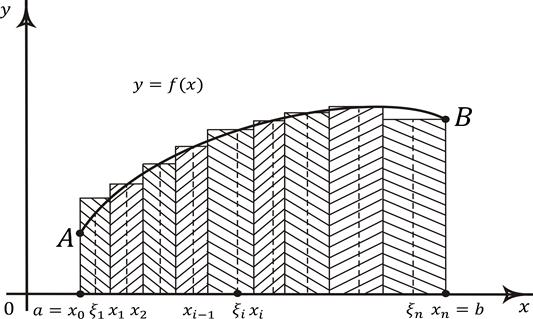
Рис. 2.1 Геометрический смысл интегральной суммы и определенного интеграла
Обозначим через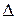 
длину наибольшего частичного отрезка разбиения:
.
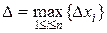Определение. Определенным интегралом от функции на отрезке называется предел интегральных сумм при стремлении к нулю длины наибольшего частичного отрезка разбиения, если этот предел существует и не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора в каждом из них точки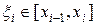 
:
.
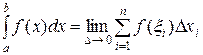Функция называется интегрируемой на отрезке . Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок – отрезком интегрирования. Функция называется также подынтегральной функцией,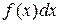 
– подынтегральным выражением, x – переменной интегрирования.
Из определения следует, что определенный интеграл представляет собой некоторое число и не зависит от обозначения переменной интегрирования:
.
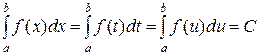Из определения определенного интеграла и рис. 2.1 следует геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции по отрезку численно равен площади криволинейной трапеции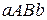 
, т.е. фигуры, ограниченной осью Ох, графиком функции 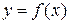и двумя прямым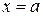и 
и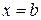 
.
Теорема 2.1 существования определенного интеграла (без доказательства).
Если функция непрерывна на отрезке , то для нее на этом отрезке существует определенный интеграл.
Замечание. Класс интегрируемых функций шире, чем класс непрерывных функций. Например, интегрируемыми являются также кусочно-непрерывные на отрезке функции.
