2015-04-23
6443
Свойство 1. Постоянный множитель можно выносить за знак интеграла:
.
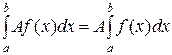Доказательство:
.
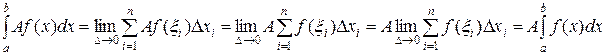Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:
.
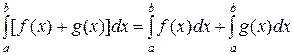Доказательство:
.
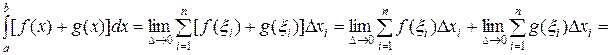
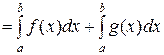Свойство 3. Если отрезок интегрирования 
разбить на два отрезка 
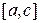и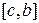 
, то интеграл по всему отрезку будет равен сумме интегралов по отрезкам 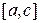и :
.
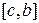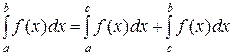Доказательство:
.
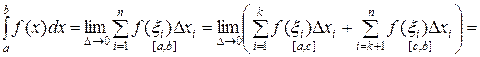
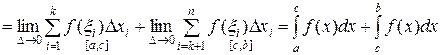Свойство 4. При перемене местами пределов интегрирования интеграл изменяет знак:
.
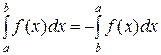Доказательство следует из определения определенного интеграла (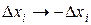
при 
).
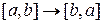Свойство 5. Интеграл с одинаковыми пределами интегрирования равен нулю:
.
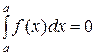Доказательство следует из свойства 4 (при 
):
.
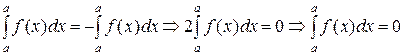Свойство 6. Интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования:
.
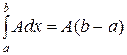Доказательство:
.
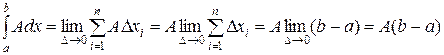Свойство 7. Если m и M – наименьшее и наибольшее значения функции 
на отрезке , то
.
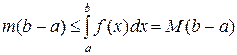Доказательство дается переходом к пределу при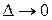 
в очевидных неравенствах:
.
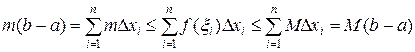Свойство 8. Абсолютная величина интеграла от данной функции не превышает интеграла от абсолютной величины этой же функции:
.
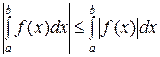Доказательство. Так как на основании свойства абсолютной величины числа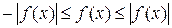 
для 
, то
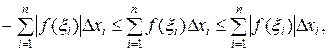
откуда при переходе к пределу при 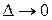получаем:
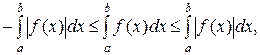
а это равносильно неравенству, которое требовалось доказать.
Свойство 9 (Теорема о среднем). Если функция непрерывна на отрезке , то на этом отрезке существует такая точка с, что справедлива формула
называемая формулой среднего значения функции на отрезке .
Доказательство. Так как функция непрерывна на отрезке , то по второй теореме Вейерштрасса
.
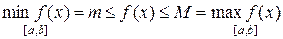Отсюда на основании свойства 7 получаем
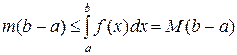или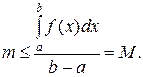 
Положим
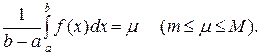
Так как функция непрерывна на отрезке , то по второй теореме Больцано-Коши на отрезке найдется такая точка с, что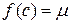 
. Поэтому
что и требовалось доказать.
