Пусть на отрезке  задана непрерывная функция
задана непрерывная функция 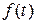 .
.
Определение. Функция
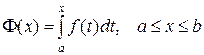
называется определенным интегралом с переменным верхним пределом.
Теорема 2.2. Производная определенного интеграла от непрерывной на отрезке  функции по переменному верхнему пределу равна значению подынтегральной функции на верхнем пределе:
функции по переменному верхнему пределу равна значению подынтегральной функции на верхнем пределе:
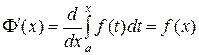 .
.
Доказательство. Дадим аргументу 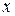 приращение
приращение 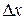 . Найдем приращение функции
. Найдем приращение функции 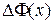 , используя свойство 3 определенного интеграла:
, используя свойство 3 определенного интеграла:
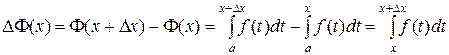 .
.
Применяя к последнему интегралу теорему о среднем (свойство 9), получим
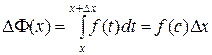 ,
,
где с заключено между 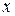 и
и 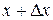 .
.
Согласно определению производной имеем
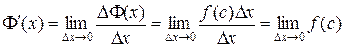 .
.
Так как 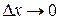 , то
, то 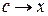 , и в силу непрерывности подынтегральной функции на отрезке
, и в силу непрерывности подынтегральной функции на отрезке 
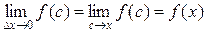 .
.
Следовательно, 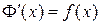 .
.
Таким образом, доказана теорема 1.2 существования первообразной для непрерывной на отрезке  функции
функции  , причем первообразной для
, причем первообразной для  является определенный интеграл с переменным верхним пределом
является определенный интеграл с переменным верхним пределом 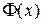 :
:
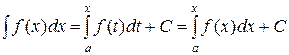 .
.
 2015-04-23
2015-04-23 936
936








