С помощью теоремы 2.2 выведем основную формулу интегрального исчисления – формулу Ньютона-Лейбница. Эта формула дает способ вычисления определенного интеграла через первообразную от подынтегральной функции, не прибегая к составлению интегральной суммы и к вычислению ее предела.
Теорема 2.3. Если 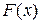 есть какая-либо первообразная от непрерывной на отрезке
есть какая-либо первообразная от непрерывной на отрезке  функции
функции  , то справедлива формула Ньютона-Лейбница:
, то справедлива формула Ньютона-Лейбница:
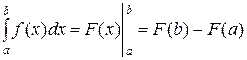 .
.
Доказательство. По теореме 2.2 функция 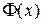 является первообразной от функции
является первообразной от функции  на отрезке
на отрезке  , т.е.
, т.е.
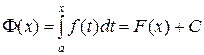 .
.
Определим постоянную С, подставляя в это равенство значение 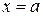 и используя свойство 5 определенного интеграла:
и используя свойство 5 определенного интеграла:
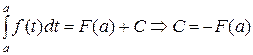 , так как
, так как 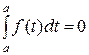 .
.
Тогда
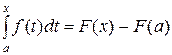 .
.
Полагая в полученном равенстве 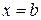 и затем заменяя переменную интегрирования t на x, получаем формулу Ньютона-Лейбница.
и затем заменяя переменную интегрирования t на x, получаем формулу Ньютона-Лейбница.
Пример
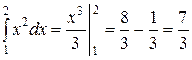 .
.
 2015-04-23
2015-04-23 1175
1175
