Теорема 2.4. Пусть  – непрерывная функция на отрезке
– непрерывная функция на отрезке  . Тогда, если: 1) функция
. Тогда, если: 1) функция 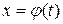 дифференцируема на отрезке
дифференцируема на отрезке 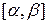 и
и 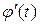 непрерывна на
непрерывна на 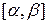 ; 2) множеством значений функции
; 2) множеством значений функции 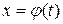 является отрезок
является отрезок  ; 3)
; 3) 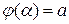 и
и 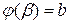 , то справедлива формула замены переменной в определенном интеграле:
, то справедлива формула замены переменной в определенном интеграле:
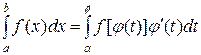 .
.
Доказательство. По формуле Ньютона-Лейбница
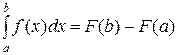 ,
,
где 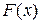 – первообразная для функции
– первообразная для функции  на отрезке
на отрезке  . Рассмотрим на отрезке
. Рассмотрим на отрезке 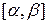 сложную функцию
сложную функцию 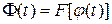 . Применяя правило дифференцирования сложной функции, находим
. Применяя правило дифференцирования сложной функции, находим
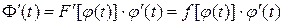 .
.
Отсюда следует, что функция 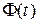 является первообразной для функции
является первообразной для функции 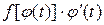 и непрерывной на отрезке
и непрерывной на отрезке 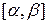 , а поэтому согласно формуле Ньютона-Лейбница получаем
, а поэтому согласно формуле Ньютона-Лейбница получаем
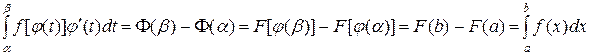 .
.
Пример
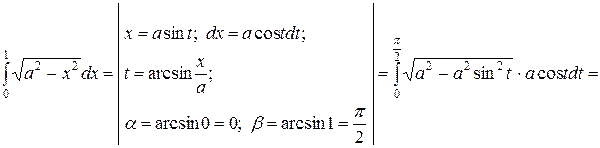
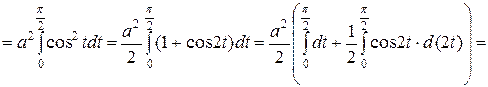
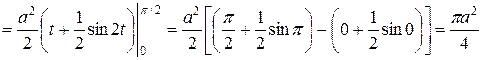 .
.
 2015-04-23
2015-04-23 1046
1046
