Интегрирование по частям в определенном интеграле

Теорема 2.5. Если функци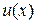и и 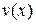имеют непрерывные производные на отрезке , то справедлива формула интегрирования по частям в определенном интеграле:

.

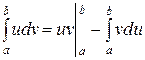Доказательство. Так как функция 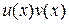является первообразной для функции 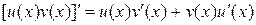, то по формуле Ньютона-Лейбница

.

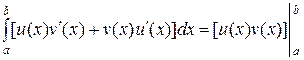Отсюда, используя свойство 2 определенного интеграла, получаем

,

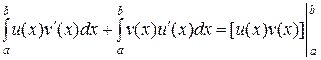или, так как 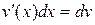и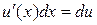

,

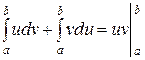откуда и следует доказываемая формула.

Пример

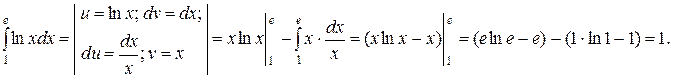
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ