2015-04-23
9149
Рассмотрим достаточные признаки сходимости несобственных интегралов (признаки сравнения), позволяющие выяснить вопрос о сходимости несобственного интеграла без знания первообразной его подынтегральной функции.
Признак сравнения 1 (без доказательства). Пусть на промежутке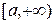 
функции 
и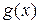 
непрерывны и удовлетворяют неравенствам 
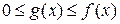. Тогда:
1) если интеграл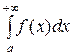 
сходится, то сходится и интеграл 
;
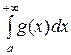2) если интеграл 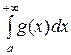расходится, то расходится и интеграл .
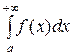Признак сравнения 2 (без доказательства). Пусть на промежутке 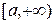функции и 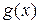непрерывны и удовлетворяют неравенствам 
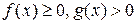. Тогда, если существует конечный и отличный от нуля предел
,
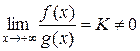то несобственные интегралы 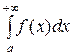и 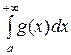оба сходятся или оба расходятся.
Замечание 1. Аналогичные признаки сравнения справедливы и для других видов несобственного интеграла первого рода, а также для несобственных интегралов второго рода.
Замечание 2. При применении признаков сравнения требуется знать несобственные интегралы, относительно которых заранее известно, сходятся они или расходятся.
В качестве таких «эталонных» интегралов на практике часто используются следующие несобственные интегралы:
1) несобственный интеграл первого рода
,
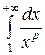
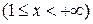который сходится при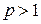 
и расходится при 
;
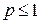2) несобственный интеграл второго рода
,
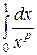
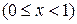который сходится при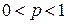 
и расходится при 
.
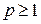Пример. Исследуем на сходимость несобственный интеграл первого рода
.
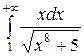Так как на промежутке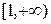 
,
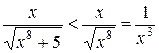а интеграл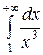 
сходится 
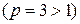, то по признаку сравнения 1 исходный интеграл также сходится.
