2015-04-23
9853
(от неограниченных функций)
Обобщим понятие определенного интеграла на случай подынтегральной функции, неограниченной на промежутке интегрирования.
Определение. Несобственным интегралом второго рода от функции 
, непрерывной на промежутке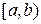 
и имеющей бесконечный разрыв при 
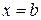, называется предел определенного интеграла 
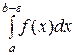с переменным верхним пределом 
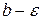при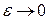 
:
.
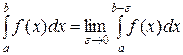Если указанный предел существует, то несобственный интеграл называется сходящимся, а если предел не существует, то расходящимся.
Из определения и рис. 3.2 следует геометрический смысл несобственного интеграла второго рода: несобственный интеграл второго рода от неотрицательной функции численно равен площади криволинейной трапеции с бесконечно длинной высотой.
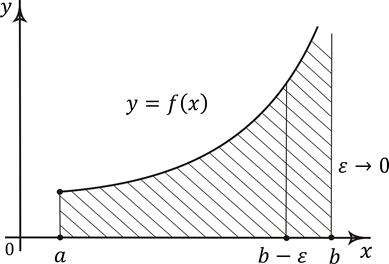
Рис. 3.2. Геометрический смысл несобственного интеграла второго рода
Аналогично вводится несобственный интеграл второго рода от функции , непрерывной на промежутке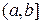 
и имеющей бесконечный разрыв при 
:
.
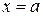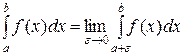Можно определить и несобственный интеграл второго рода от функции , имеющей бесконечный разрыв в некоторой внутренней точке с промежутка 
:
.
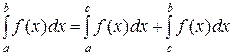Пример
,
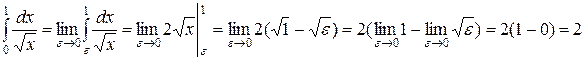т.е. данный интеграл сходится.
