Определение. Несобственный интеграл называется абсолютно сходящимся, если сходится несобственный интеграл от абсолютной величины подынтегральной функции.
Несобственный интеграл называется условно сходящимся, если он сходится, а несобственный интеграл от абсолютной величины подынтегральной функции расходится.
Теорема 3.1 (без доказательства). Абсолютно сходящийся интеграл сходится.
Используя понятие абсолютной сходимости и данную теорему, можно исследовать сходимость несобственных интегралов от знакопеременных функций, применяя признаки сравнения.
Пример. Исследуем на сходимость несобственный интеграл первого рода
от знакопеременной функции
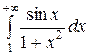 .
.
Так как на промежутке 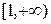
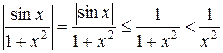 ,
,
и интеграл 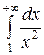 сходится
сходится 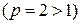 , то по признаку сравнения 1 исходный интеграл также сходится (абсолютно).
, то по признаку сравнения 1 исходный интеграл также сходится (абсолютно).
 2015-04-23
2015-04-23 2829
2829
