Определение. Уравнение вида
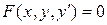 ,
,
где x – независимая переменная, y – искомая функция, 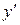 – ее производная, называется дифференциальным уравнением первого порядка.
– ее производная, называется дифференциальным уравнением первого порядка.
Если это уравнение можно разрешить относительно 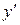 , то оно принимает вид
, то оно принимает вид
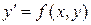 или
или 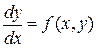
и называется уравнением первого порядка, разрешенным относительно производной.
Будем рассматривать именно такие уравнения и, вообще говоря, считать, что переменные x и y в нем равноправны, т.е. каждую из них можно рассматривать как функцию другой.
Пример
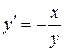 или
или 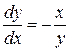 или
или 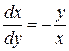 .
.
Определение. Общим решением дифференциального уравнения первого порядка называется семейство функций
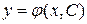 ,
,
обращающих дифференциальное уравнение в тождество при любом значении произвольной постоянной C.
Определение. Общим интегралом дифференциального уравнения первого порядка называется семейство функций
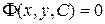 ,
,
обращающих дифференциальное уравнение в тождество при любом значении произвольной постоянной C.
Определение. Частным решением дифференциального уравнения первого порядка называется любая функция
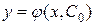 ,
,
получаемая из общего решения при задании определенного значения 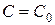 произвольной постоянной C.
произвольной постоянной C.
Определение. Частным интегралом дифференциального уравнения первого порядка называется любая функция
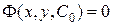 ,
,
получаемая из общего интеграла при задании определенного значения 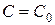 произвольной постоянной C.
произвольной постоянной C.
Пример. Уравнение 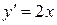 имеет общее решение
имеет общее решение 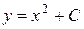 и частное решение
и частное решение 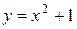 при
при 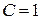 .
.
Действительно, подстановка 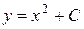 в исходное уравнение
в исходное уравнение 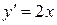 дает
дает
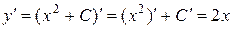 ,
,
т.е. тождество 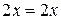 при любом значении произвольной постоянной C.
при любом значении произвольной постоянной C.
Геометрически общее решение 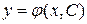 представляет собой однопараметрическое (C – параметр) семейство кривых на плоскости Oxy. Эти кривые называются интегральными кривыми данного дифференциального уравнения, причем частному решению
представляет собой однопараметрическое (C – параметр) семейство кривых на плоскости Oxy. Эти кривые называются интегральными кривыми данного дифференциального уравнения, причем частному решению 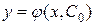 соответствует одна кривая этого семейства при значении параметра
соответствует одна кривая этого семейства при значении параметра 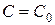 .
.
Определение. Условие, что при 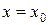 функция
функция 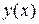 должна равняться заданному числу
должна равняться заданному числу 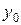 , называется начальным условием:
, называется начальным условием:
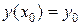 или
или 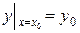 .
.
Определение. Задача, в которой требуется найти частное решение дифференциального уравнения 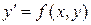 , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию 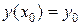 , называется задачей Коши или начальной задачей для дифференциального уравнения первого порядка.
, называется задачей Коши или начальной задачей для дифференциального уравнения первого порядка.
С геометрической точки зрения решить задачу Коши – значит из множества интегральных кривых выделить ту, которая проходит через заданную точку 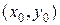 плоскости Oxy.
плоскости Oxy.
Ответ на вопрос о том, при каких условиях, налагаемых на функцию 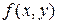 , задача Коши имеет решение, дает теорема Коши, которая называется теоремой существования и единственности решения дифференциального уравнения
, задача Коши имеет решение, дает теорема Коши, которая называется теоремой существования и единственности решения дифференциального уравнения 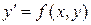 .
.
Теорема 4.1 (теорема Коши) (без доказательства). Если в уравнении 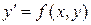 функция
функция 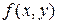 и ее частная производная
и ее частная производная 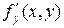 определены и непрерывны в некоторой области D плоскости Oxy, то, какова бы ни была внутренняя точка
определены и непрерывны в некоторой области D плоскости Oxy, то, какова бы ни была внутренняя точка 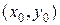 области D, в некоторой окрестности этой точки существует единственное решение
области D, в некоторой окрестности этой точки существует единственное решение 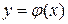 данного уравнения, удовлетворяющее условию
данного уравнения, удовлетворяющее условию 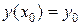 .
.
Геометрически теорема Кошиутверждает, что через каждую внутреннюю точку 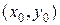 области D проходит единственная интегральная кривая.
области D проходит единственная интегральная кривая.
Пример. Рассмотрим дифференциальное уравнение 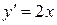 .
.
Данное уравнение удовлетворяет условиям теоремы Коши на всей плоскости Oxy, так как функция 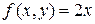 и
и 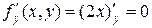 определены и непрерывны на всей плоскости Oxy. Легко проверить (см. предыдущий пример), что функция
определены и непрерывны на всей плоскости Oxy. Легко проверить (см. предыдущий пример), что функция 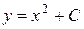 , где C – произвольная постоянная, является общим решением данного уравнения на всей плоскости Oxy
, где C – произвольная постоянная, является общим решением данного уравнения на всей плоскости Oxy 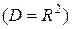 .
.
Геометрически (рис. 4.1) это общее решение представляет собой семейство парабол.
Для решения какой-нибудь задачи Коши, т.е. отыскания частного решения, зададим конкретное начальное условие: 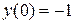 .
.
Подставляя эти значения 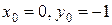 в общее решение
в общее решение 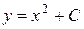 , получаем
, получаем 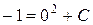 , откуда
, откуда 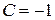 .
.
Таким образом, найдено частное решение (решение задачи Коши) 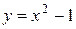 . Геометрически это означает, что из семейства интегральных кривых – парабол
. Геометрически это означает, что из семейства интегральных кривых – парабол 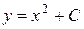 – выбрана одна
– выбрана одна 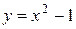 , проходящая через точку (0;-1) (рис. 4.1).
, проходящая через точку (0;-1) (рис. 4.1).
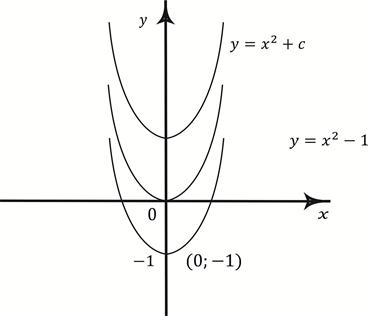
Рис. 4.1 Геометрический смысл общего и частного решений уравнения 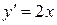
Определение. Точки плоскости, в которых не выполняются условия теоремы существования и единственности решения, называются особыми точками дифференциального уравнения.
Если график некоторого решения (интегральная кривая) сплошь состоит из особых точек, то решение называется особым.
Особое решение не может быть получено из общего решения ни при каких значениях произвольной постоянной C.
 2015-04-23
2015-04-23 2479
2479
