2015-04-23
679
Определение. Уравнением с разделяющимися переменными называется дифференциальное уравнение первого порядка вида
,
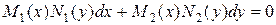где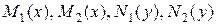 
– заданные функции своих переменных.
Метод решения. Разделив обе части уравнения на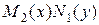 
и почленно взяв квадратуры (проинтегрировав), получим общий интеграл уравнения:
;
.
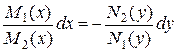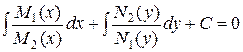Замечание. Прямые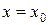 
и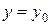 
будут интегральными кривыми уравнения с разделяющимися переменными, есл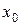и 
и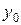 
являются соответственно корнями уравнени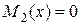й 
и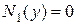 
.
Пример. Решить уравнение
.
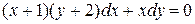Разделим обе части уравнения на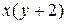 
и получим общий интеграл уравнения:
;
;
.
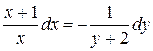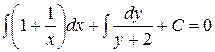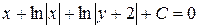Так как прямые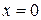 
и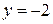 
обращают выражение 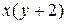в нуль, то они также будут решениями.
