Определение. Уравнением Бернулли называется дифференциальное уравнение первого порядка вида
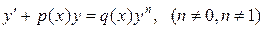 ,
,
где p (x) и q (x) – заданные функции.
Метод решения. С помощью подстановки 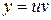 , где
, где 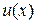 и
и 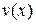 – две неизвестные функции, уравнение преобразуется к виду
– две неизвестные функции, уравнение преобразуется к виду
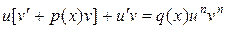
и сводится к двум уравнениям с разделяющимися переменными относительно каждой из неизвестных функций u и v:
1) 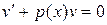 ; 2)
; 2) 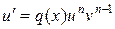 .
.
Из первого уравнения определяем 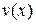 и, подставляя его во второе уравнение, определяем
и, подставляя его во второе уравнение, определяем 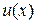 , после чего находим общее решение
, после чего находим общее решение 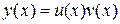 исходного уравнения Бернулли. При этом при решении первого уравнения полагаем аддитивную постоянную C равной нулю.
исходного уравнения Бернулли. При этом при решении первого уравнения полагаем аддитивную постоянную C равной нулю.
Пример. Решить уравнение
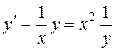 .
.
Используя подстановку 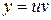 , находим общее решение:
, находим общее решение:
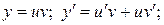
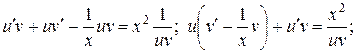
1) 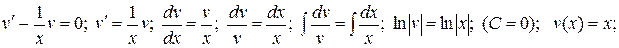
2) 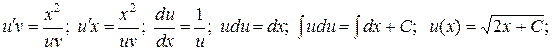
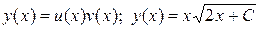 .
.
 2015-04-23
2015-04-23 597
597








