1) Уравнение вида 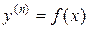 .
.
Метод решения. Общее решение уравнения находится n -кратным интегрированием (последовательным взятием квадратур).
Пример. Найти общее решение уравнения
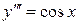 .
.
Последовательно интегрируя почленно исходное уравнение три раза (беря квадратуры), находим общее решение:
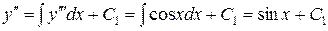 ,
,
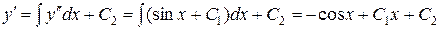 ,
,
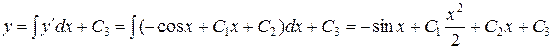 .
.
2) Уравнение вида 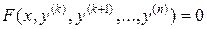 .
.
Метод решения. Уравнение не содержит явно искомой функции y и ее производных до порядка 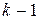 включительно, поэтому с помощью подстановки
включительно, поэтому с помощью подстановки 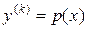 порядок уравнения понижается на k единиц:
порядок уравнения понижается на k единиц:
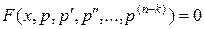 ,
,
так как
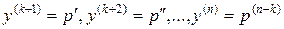 .
.
Если для вновь полученного уравнения можно найти общее решение
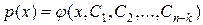 ,
,
то общее решение исходного уравнения получается путем k -кратного интегрирования функции
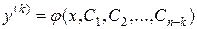 .
.
В частности, если уравнение 2-го порядка не содержит y, то замена переменных 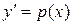 приводит к уравнению 1-го порядка.
приводит к уравнению 1-го порядка.
Пример. Найти общее решение дифференциального уравнения
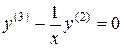 .
.
Так как исходное уравнение не содержит 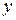 и
и 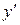 , то сделаем подстановку
, то сделаем подстановку 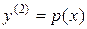 . Тогда
. Тогда 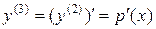 и из исходного уравнения 3-го порядка получаем уравнение 1-го порядка
и из исходного уравнения 3-го порядка получаем уравнение 1-го порядка
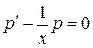 ,
,
которое является уравнением с разделяющимися переменными 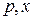 . Находим его общее решение
. Находим его общее решение
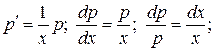
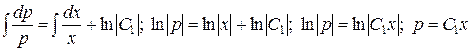 .
.
Теперь найдем общее решение исходного уравнения путем двукратного интегрирования функции
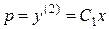 .
.
Получаем:
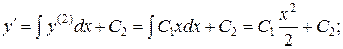
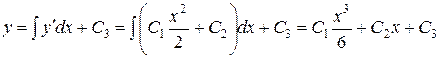 .
.
3) Уравнение вида 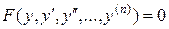 .
.
Метод решения. Уравнение не содержит явно независимой переменной x, поэтомус помощью подстановки 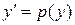 порядок уравнения понижается наединицу:
порядок уравнения понижается наединицу:
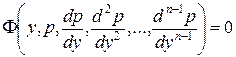 ,
,
так как производные 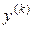 выражаются при этом через производные порядка не выше
выражаются при этом через производные порядка не выше 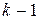 от p по y. Действительно, по правилу дифференцирования сложной функции получаем
от p по y. Действительно, по правилу дифференцирования сложной функции получаем
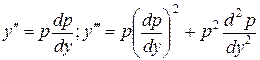 и т.д.
и т.д.
Пример. Найти общее решение дифференциального уравнения
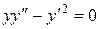 .
.
Так как исходное уравнение не содержит явно независимой переменной x, то сделаем подстановку 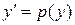 . Тогда
. Тогда 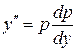 и из исходного уравнения 2-го порядка получаем уравнение 1-го порядка
и из исходного уравнения 2-го порядка получаем уравнение 1-го порядка
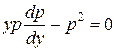 ,
,
которое является уравнением с разделяющимися переменными 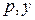 . Находим его общее решение:
. Находим его общее решение:
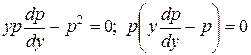 ;
;
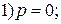
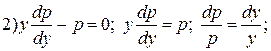
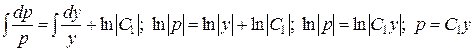 .
.
Теперь найдем общее решение исходного уравнения:
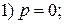
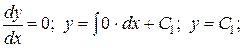
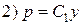 ;
;
 2015-04-23
2015-04-23 1071
1071
