Определение. Уравнение вида
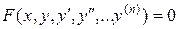 ,
,
где x – независимая переменная, y – искомая функция, 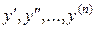 – ее производные, называется дифференциальным уравнением высшего (n-го) порядка.
– ее производные, называется дифференциальным уравнением высшего (n-го) порядка.
Если это уравнение можно разрешить относительно старшей производной 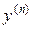 , то оно принимает вид
, то оно принимает вид
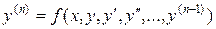
и называется уравнением высшего порядка, разрешенным относительно старшей производной.
В дальнейшем будем рассматривать именно такие уравнения.
Пример. Уравнение высшего (третьего) порядка, разрешенное относительно старшей (третьей) производной:
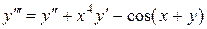 .
.
Определение. Общим решением дифференциального уравнения высшего порядка называется семейство функций
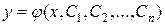 ,
,
обращающих дифференциальное уравнение в тождество при любых значениях произвольных постоянных 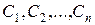 .
.
Определение. Общим интегралом дифференциального уравнения высшего порядка называется семейство функций
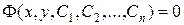 ,
,
обращающих дифференциальное уравнение в тождество при любых значениях произвольных постоянных 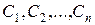 .
.
Определение. Частным решением дифференциального уравнения высшего порядка называется любая функция
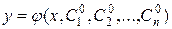 ,
,
получаемая из общего решения при задании определенных значений всем n произвольным постоянным: 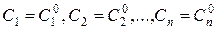 .
.
Определение. Частным интегралом дифференциального уравнения высшего порядка называется любая функция
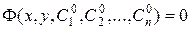 ,
,
получаемая из общего интеграла при задании определенных значений всем n произвольным постоянным: 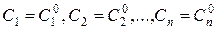 .
.
Определение. Условия, что при 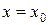 функция
функция 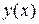 и ее производные
и ее производные 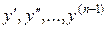 должны равняться заданным числам
должны равняться заданным числам 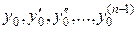 соответственно, называются начальными условиями для дифференциального уравнения высшего (n -го) порядка:
соответственно, называются начальными условиями для дифференциального уравнения высшего (n -го) порядка:
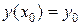 ,
, 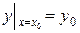 ,
,
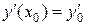 ,
, 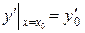 ,
,
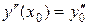 , или
, или 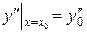 ,
,
………….. …………..
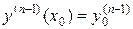 ,
, 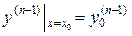 .
.
Определение. Задача, в которой требуется найти частное решение дифференциального уравнения
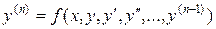 ,
,
удовлетворяющее заданным начальным условиям
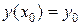 ,
,
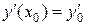 ,
,
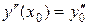 ,
,
…………..
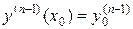 ,
,
называется задачей Коши или начальной задачей для дифференциального уравнения высшего (n -го) порядка.
Ответ на вопрос о том, при каких условиях, налагаемых на функцию 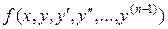 , задача Коши имеет решение, дает теорема Коши, которая называется теоремой существования и единственности решения дифференциального уравнения
, задача Коши имеет решение, дает теорема Коши, которая называется теоремой существования и единственности решения дифференциального уравнения 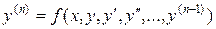 .
.
Теорема 4.2 (теорема Коши) (без доказательства). Если в уравнении 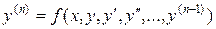 функция
функция 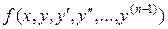 и ее частные производные первого порядка по аргументам
и ее частные производные первого порядка по аргументам 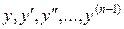 определены и непрерывны в некоторой области
определены и непрерывны в некоторой области 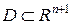 , то, какова бы ни была внутренняя точка
, то, какова бы ни была внутренняя точка 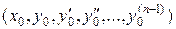 области D, в некоторой окрестности этой точки существует единственное решение
области D, в некоторой окрестности этой точки существует единственное решение 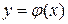 данного уравнения, удовлетворяющее условиям
данного уравнения, удовлетворяющее условиям
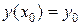 ,
,
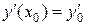 ,
,
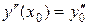 ,
,
…………..
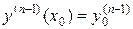 .
.
Пример. Найти общее решение дифференциального уравнения третьего порядка
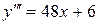
и выделить из полученного общего решения частное решение, удовлетворяющее начальным условиям:
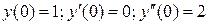 .
.
Последовательно интегрируя почленно исходное уравнение (беря квадратуры), находим общее решение:
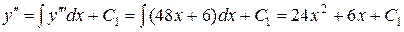 ,
,
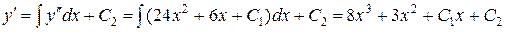 ,
,
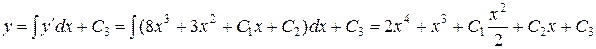 .
.
Это решение зависит от трех произвольных постоянных 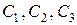 . Определим их, подставляя в полученные соотношения начальные условия:
. Определим их, подставляя в полученные соотношения начальные условия:
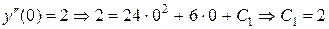 ;
;
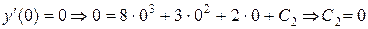 ;
;
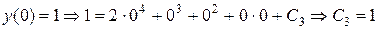 .
.
Таким образом, частное решение, удовлетворяющее заданным начальным условиям, имеет вид
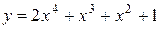 .
.
Наряду с основной начальной задачей часто приходится решать так называемые краевые или граничные задачи. В этих задачах значения искомой функции и/или ее производных задаются не в одной, а в двух точках, ограничивающих отрезок, на котором требуется определить решение. При этом число заданных краевых условий обычно равно порядку дифференциального уравнения. Для каждого класса краевых задач, как и для задачи Коши, требуется решать вопрос о существовании и единственности решения.
Пример. Найти решение дифференциального уравнения 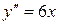 , удовлетворяющее на отрезке
, удовлетворяющее на отрезке 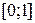 краевым условиям:
краевым условиям: 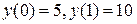 .
.
Последовательно интегрируя почленно исходное уравнение (беря квадратуры), находим общее решение:
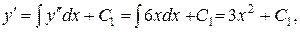
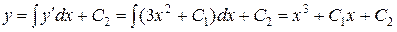 .
.
Это решение зависит от двух произвольных постоянных C 1 и C 2. Определим их, подставляя в полученные соотношения краевые условия:
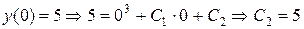 ;
;
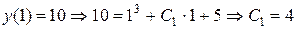 .
.
Таким образом, искомое решение, удовлетворяющее заданным краевым условиям, имеет вид
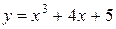 .
.
 2015-04-23
2015-04-23 7580
7580
