Определение. Линейным дифференциальным уравнением высшего (n-го) порядка называется уравнение, линейное относительно неизвестной функции 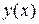 и ее производных
и ее производных
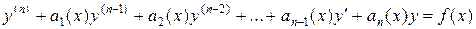 .
.
Функции 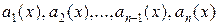 называются коэффициентами уравнения. Функция
называются коэффициентами уравнения. Функция  называется правой частью уравнения.
называется правой частью уравнения.
Если 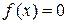 , то уравнение называется линейным однородным уравнением или уравнением без правой части.
, то уравнение называется линейным однородным уравнением или уравнением без правой части.
Если же 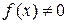 , то уравнение называется линейным неоднородным уравнением или уравнением с правой частью.
, то уравнение называется линейным неоднородным уравнением или уравнением с правой частью.
Примеры
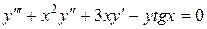 – линейное однородное уравнение 3-го порядка.
– линейное однородное уравнение 3-го порядка.
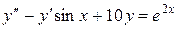 – линейное неоднородное уравнение 2-го порядка.
– линейное неоднородное уравнение 2-го порядка.
Из определения линейного однородного уравнения и свойств линейности производных следует очевидное свойство решений линейного однородного уравнения: линейная комбинация решений линейного однородного уравнения является решением того же уравнения.
Из определения линейного неоднородного уравнения и свойств линейности производных следует очевидное свойство решений линейного неоднородного уравнения: сумма решений линейного неоднородного уравнения и соответствующего (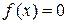 ) однородного уравнения является решением неоднородного уравнения.
) однородного уравнения является решением неоднородного уравнения.
Выясним структуру общих решений линейного однородного уравнения и линейного неоднородного уравнения.
Теорема 4.3 (без доказательства). Общим решением на отрезке  линейного однородного уравнения
линейного однородного уравнения
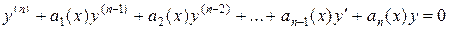
с непрерывными на отрезке  коэффициентами
коэффициентами 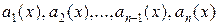 является линейная комбинация
является линейная комбинация
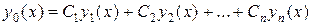
n линейно независимых на том же отрезке частных решений этого уравнения 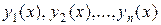 .
.
Теорема 4.4 (без доказательства). Общее решение на отрезке  линейного неоднородного уравнения
линейного неоднородного уравнения
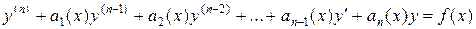
с непрерывными на отрезке  коэффициентами
коэффициентами 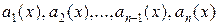 и непрерывной правой частью
и непрерывной правой частью  равно сумме общего решения
равно сумме общего решения
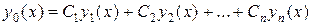
соответствующего однородного уравнения
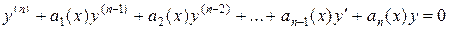
и какого-нибудь частного решения 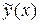 неоднородного уравнения:
неоднородного уравнения:
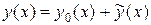 .
.
 2015-04-23
2015-04-23 2463
2463
