Определение. Система обыкновенных дифференциальных уравнений вида
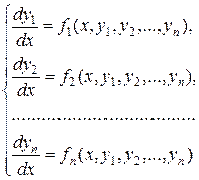
относительно искомых функций 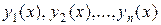 называется нормальной системой дифференциальных уравнений.
называется нормальной системой дифференциальных уравнений.
Определение. Решением нормальной системы дифференциальных уравнений называется совокупность функций 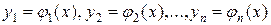 ,
,
обращающих каждое уравнение системы в верное равенство (тождество).
Определение. Общим решением нормальной системы дифференциальных уравнений называется совокупность функций
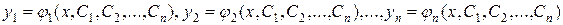 ,
,
обращающих каждое уравнение системы в верное равенство (тождество) при любых значениях произвольных постоянных 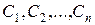 .
.
Определение. Частным решением нормальной системы дифференциальных уравнений называется любая совокупность функций
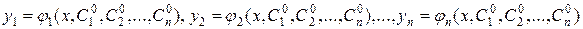 ,
,
получаемая из общего решения при задании определенных значений всем n произвольным постоянным 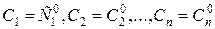 .
.
Определение. Условия вида
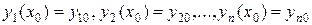 ,
,
где 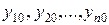 – заданные числа, называются начальными условиями для нормальной системы дифференциальных уравнений.
– заданные числа, называются начальными условиями для нормальной системы дифференциальных уравнений.
Определение. Задача, в которой требуется найти частное решение нормальной системы дифференциальных уравнений
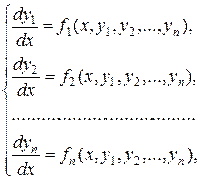
удовлетворяющее заданным начальным условиям
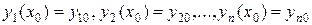 ,
,
называется задачей Коши или начальной задачей для нормальной системы дифференциальных уравнений.
Ответ на вопрос о том, при каких условиях, налагаемых на функции 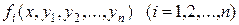 , задача Коши имеет решение, дает теорема Коши, которая называется теоремой существования и единственности решения для нормальной системы дифференциальных уравнений.
, задача Коши имеет решение, дает теорема Коши, которая называется теоремой существования и единственности решения для нормальной системы дифференциальных уравнений.
Теорема 5.1 (теорема Коши) (без доказательства). Если правые части 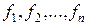 уравнений нормальной системы определены и непрерывны в некоторой области
уравнений нормальной системы определены и непрерывны в некоторой области 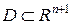 и имеют в ней непрерывные частные производные
и имеют в ней непрерывные частные производные
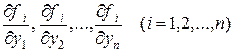 ,
,
то, какова бы ни была внутренняя точка 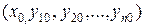 области D, в некоторой окрестности этой точки существует единственное решение
области D, в некоторой окрестности этой точки существует единственное решение 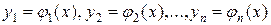 нормальной системы, удовлетворяющее начальным условиям
нормальной системы, удовлетворяющее начальным условиям 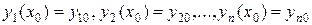 .
.
 2015-04-23
2015-04-23 6918
6918
