Определение. Линейным однородным дифференциальным уравнением высшего (n-го) порядка с постоянными коэффициентами называется уравнение вида
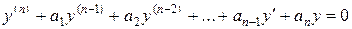 ,
,
где коэффициенты 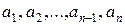 – заданные действительные числа.
– заданные действительные числа.
Метод решения. Согласно теореме 4.3 общим решением 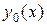 на отрезке
на отрезке  линейного однородного дифференциального уравнения высшего порядка с постоянными коэффициентами является линейная комбинация
линейного однородного дифференциального уравнения высшего порядка с постоянными коэффициентами является линейная комбинация
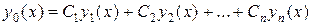
–линейно независимых на том же отрезке частных решений этого уравнения 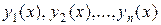 .
.
Для их нахождения составляется и решается характеристическое уравнение
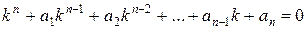 ,
,
получаемое заменой в исходном дифференциальном уравнении производных 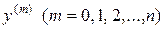 искомой функции степенями
искомой функции степенями 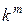 , причем сама функция
, причем сама функция 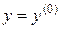 заменяется единицей. Характеристическое уравнение – это алгебраическое уравнение степени n.
заменяется единицей. Характеристическое уравнение – это алгебраическое уравнение степени n.
Каждому из n корней характеристического уравнения соответствует одно из n линейно независимых частных решений линейного однородного дифференциального уравнения, причем:
– каждому действительному простому корню k соответствует частное решение вида
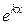 ;
;
– каждому действительному корню k кратности 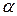 соответствуют
соответствуют 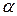 частных решений вида
частных решений вида
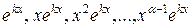 ;
;
– каждой паре комплексных сопряженных простых корней 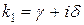 и
и 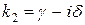 соответствует два частных решения вида
соответствует два частных решения вида
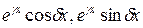 ;
;
– каждой паре комплексных сопряженных корней 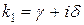 и
и 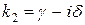 кратности
кратности 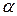 соответствуют 2
соответствуют 2 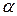 частных решений вида
частных решений вида
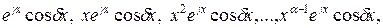
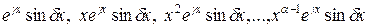 .
.
Составляя линейную комбинацию из найденных частных решений, получаем общее решение линейного однородного уравнения с постоянными коэффициентами.
Примеры
1) Найти общее решение однородного дифференциального уравнения 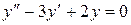 .
.
Характеристическое уравнение и его решения:
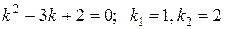 – два действительных простых корня.
– два действительных простых корня.
Частные решения однородного дифференциального уравнения:
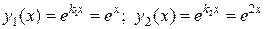 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
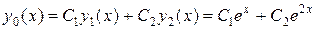 .
.
2) Найти общее решение однородного дифференциального уравнения
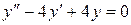 .
.
Характеристическое уравнение и его решения:
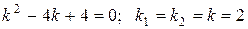 – двукратный действительный корень.
– двукратный действительный корень.
Частные решения однородного дифференциального уравнения:
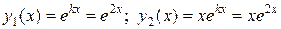 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
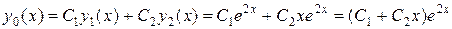 .
.
3) Найти общее решение однородного дифференциального уравнения
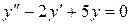 .
.
Характеристическое уравнение и его решения:
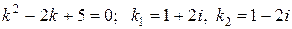 – пара комплексно сопряженных простых корней
– пара комплексно сопряженных простых корней 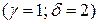 .
.
Частные решения однородного дифференциального уравнения:
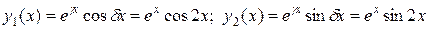 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
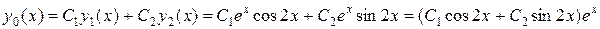 .
.
4) Найти общее решение однородного дифференциального уравнения
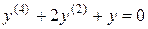 .
.
Характеристическое уравнение и его решения:
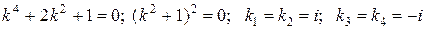 – двукратные комплексно сопряженные корни
– двукратные комплексно сопряженные корни 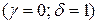 .
.
Частные решения однородного дифференциального уравнения:
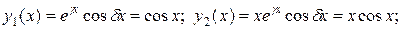
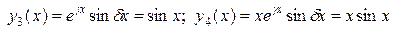 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
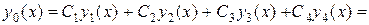
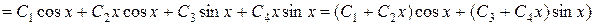 .
.
 2015-04-23
2015-04-23 2593
2593
