Определение. Нормальной системой линейных дифференциальных уравнений с постоянными коэффициентами называется нормальная система вида
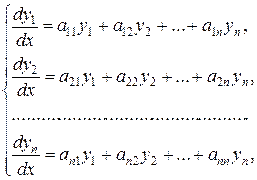
где коэффициенты 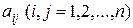 – заданные действительные числа.
– заданные действительные числа.
Нормальную систему линейных дифференциальных уравнений с постоянными коэффициентами удобно записывать в векторно-матричной форме
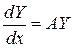 ,
,
где
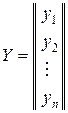 ,
, 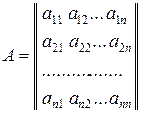 .
.
Для рассматриваемой нормальной системы имеет место теорема о структуре общего решения, аналогичная теореме 4.3 для линейного однородного дифференциального уравнения высшего порядка с постоянными коэффициентами. Именно, общим решением 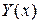 нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами является линейная комбинация
нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами является линейная комбинация
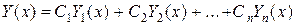
n линейно независимых частных решений этой системы
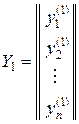 ,
, 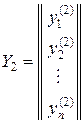 , …,
, …, 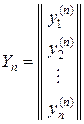 .
.
Для их нахождения составляется и решается характеристическое уравнение
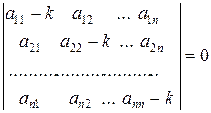 ,
,
представляющее собой алгебраическое уравнение n -ой степени относительно k.
Ограничимся случаем, когда характеристическое уравнение имеет различные (простые) действительные корни 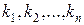 . Тогда каждому из n корней
. Тогда каждому из n корней 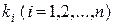 характеристического уравнения соответствует одно из n линейно независимых частных решений вида
характеристического уравнения соответствует одно из n линейно независимых частных решений вида
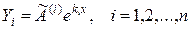 ,
,
причем элементы матрицы
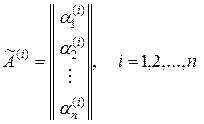
находятся из системы уравнений
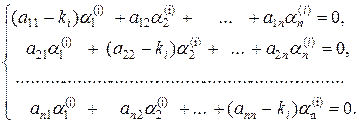
Следует заметить, что элементы 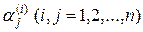 определяются из этой системы для каждого
определяются из этой системы для каждого 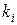 неоднозначно, так как определитель системы равен нулю (см. характеристическое уравнение) и, следовательно, по крайней мере одно уравнение является следствием остальных. Неоднозначность определения
неоднозначно, так как определитель системы равен нулю (см. характеристическое уравнение) и, следовательно, по крайней мере одно уравнение является следствием остальных. Неоднозначность определения 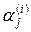 связана с тем, что решение нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами остается решением той же системы при умножении на произвольный постоянный множитель.
связана с тем, что решение нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами остается решением той же системы при умножении на произвольный постоянный множитель.
Взяв линейную комбинацию найденных линейно независимых частных решений
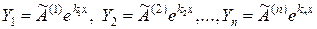 ,
,
получаем общее решение нормальной системы
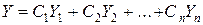
или в векторно-матричной форме
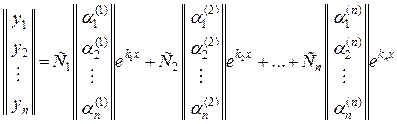 .
.
Пример. Найти общее решение системы
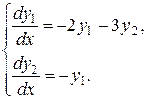
Составим и решим характеристическое уравнение
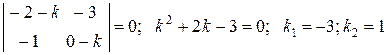 .
.
Частные решения нормальной системы, соответствующие найденным корням, имеют вид
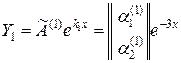 ;
;
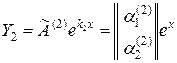 .
.
Система уравнений для определения элементов матрицы 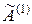 при
при 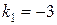 запишется таким образом:
запишется таким образом:
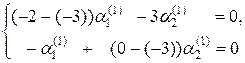 или
или 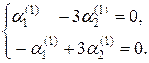
Эта система имеет бесчисленное множество решений, так как второе уравнение есть следствие первого. Полагая, например, 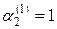 , находим
, находим 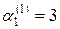 .
.
Итак, корню характеристического уравнения 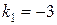 соответствует частное решение
соответствует частное решение
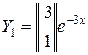 .
.
Система уравнений для определения элементов матрицы 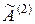 при
при 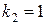 запишется таким образом:
запишется таким образом:
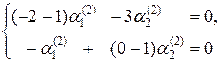 или
или 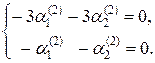
Эта система имеет бесчисленное множество решений, так как второе уравнение есть следствие первого. Полагая, например, 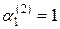 , находим
, находим 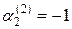 .
.
Итак, корню характеристического уравнения 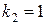 соответствует частное решение
соответствует частное решение
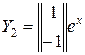 .
.
Общее решение исходной нормальной системы имеет вид
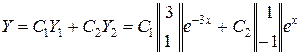
или
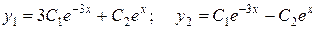 .
.
 2015-04-23
2015-04-23 633
633







