Понятие устойчивости решения нормальной системы по Ляпунову

Рассмотрим нормальную систему дифференциальных уравнений

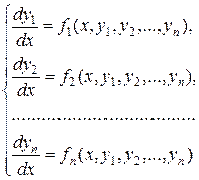
с начальными условиями в точке .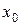

Определение. Решение 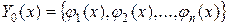нормальной системы называется устойчивым по Ляпунову, если для любого 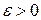найдется такое 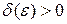, что для любого решения 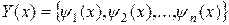той же системы, начальные значения которого в точке 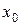удовлетворяют неравенствам

,

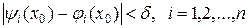для всех 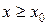справедливы неравенства

.

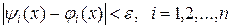Если решение 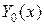устойчиво по Ляпунову и, кроме того,

,

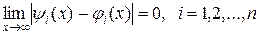то оно называется асимптотически устойчивым.

Замечание. Исследование на устойчивость решения 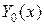нормальной системы может быть сведено к исследованию на устойчивость тривиального нулевого решения – точки покоя некоторой нормальной системы, аналогичной исходной нормальной системе.

Можно доказать, что точка покоя заведомо устойчива по Ляпунову (асимптотически устойчива) для нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами

,

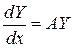если все корни характеристического уравнения системы имеют отрицательные действительные части.

Пример. Исследовать на устойчивость точку покоя системы

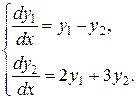
Характеристическое уравнение системы

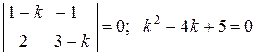
имеет пару комплексно сопряженных простых корней .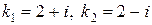

Действительная часть этих корней положительна (равна двум), поэтому точка покоя 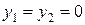является неустойчивой.