Формула Грина

Формула Грина устанавливает связь между двойным интегралом по некоторой плоской замкнутой области и криволинейным интегралом второго рода по границе этой области.

Определение. Замкнутая плоская область называется правильной, если ее граница пересекается с прямыми, параллельными осям координат, не более чем в двух точках.

Теорема 7.3 (без доказательства). Если функци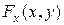и и 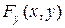непрерывны вместе со своими частными производными 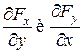в правильной области 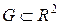с границей L, то имеет место формула Грина:

.

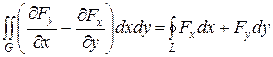Замечание. Формула Грина остается справедливой для всякой замкнутой области G, которую можно разбить на конечное число правильных областей.