2015-04-23
13287
Пусть функция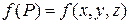 
определена и непрерывна на некоторой поверхности 
в пространстве 
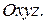Разобьем поверхность произвольным образом на n частей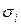 
с площадями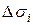 
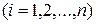(рис. 8.1). В каждой частичной области 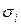выберем произвольную точку 
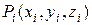и составим сумму
,
которую назовем интегральной суммой для функции 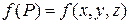в области (на поверхности) . Обозначим через 
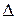наибольший из диаметров частичных областей :
.
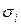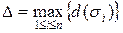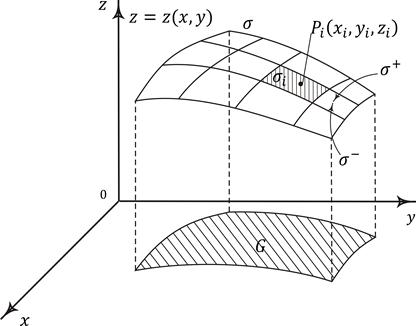
Рис. 8.1. Разбиение поверхности на частичные области в случае
поверхностного интеграла первого рода
Определение. Поверхностным интегралом первого рода от функции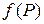 
по поверхности называется предел интегральных сумм при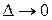 
, если этот предел существует и не зависит ни от способа разбиения поверхности на частичные области 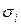, ни от выбора в каждой из них точки 
:
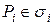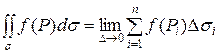
или в другой записи:
.
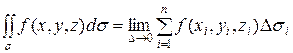Функция 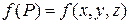называется интегрируемой по поверхности , сама – поверхностью интегрирования.
Определение. Поверхность называется гладкой, если в каждой ее точке существует касательная плоскость и при переходе от точки к точке положение этой касательной плоскости меняется непрерывно.
|
|
|
Поверхность, состоящая из конечного числа гладких кусков, которые соединены непрерывно, называется кусочно-гладкой.
Теорема 8.1 (существования поверхностного интеграла первого рода) (без доказательства). Функция 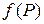, непрерывная на кусочно-гладкой поверхности , интегрируема по этой поверхности.
Замечание. Если положить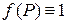 
всюду на поверхности , то из определения поверхностного интеграла первого рода легко получить формулу для вычисления площади S поверхности с помощью поверхностного интеграла первого рода:
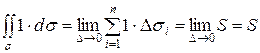
или
.
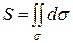Основные свойства поверхностного интеграла первого рода аналогичны соответствующим свойствам криволинейного интеграла первого рода:
Свойство 1. Постоянный множитель можно выносить за знак интеграла:
.
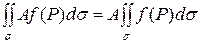Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:
.
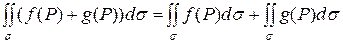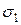Свойство 3. Если поверхность разбить на две поверхности 
и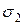 
, то интеграл по всей поверхности будет равен сумме интегралов по поверхностям 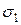и :
.
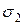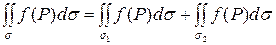Свойство 4 (Теорема о среднем). Если функция 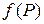непрерывна вдоль гладкой поверхности , то на этой поверхности существует такая точка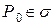 
, что справедлива формула
,
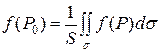где S – площадь поверхности .
Свойство 5. При изменении стороны поверхности интегрирования величина интеграла не изменяется:
,
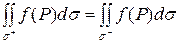где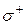 
и 
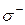– стороны поверхности интегрирования .
Вычисление поверхностного интеграла первого рода сводится к вычислению двойного интеграла следующим способом.
Если поверхность задана уравнением 
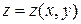и область G – проекция поверхности на плоскость Oxy (рис. 8.1), то
|
|
|
.
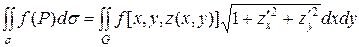Аналогично записываются формулы, выражающие интеграл по поверхности через двойные интегралы по проекциям на плоскости Oyz и Oxz.
Пример. Вычислить поверхностный интеграл первого рода
,
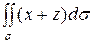где – часть плоскости 
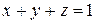, лежащая в первом октанте (рис. 8.2).
Из уравнения поверхности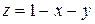 
имеем
.
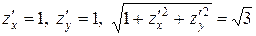Поверхность проектируется на плоскость Oxy в область G, ограниченную прямыми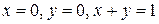 
.
По формуле вычисления поверхностного интеграла первого рода имеем:
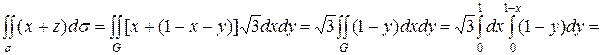
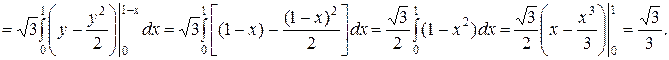
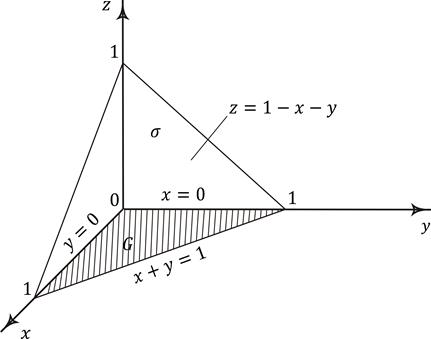
Рис. 8.2. Пример вычисления поверхностного интеграла первого рода
