2015-04-23
2479
Правила делителя напряжения и делителя тока, удобные для практического использования при расчетах, рассмотрим на примере последовательной и параллельной резистивных цепей. Из (11) следует:
.
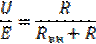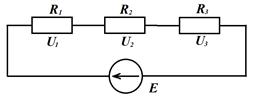
Тогда для напряжений на элементах последовательной цепи получим:
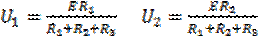
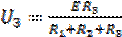
Отсюда следует правило делителя напряжения:
отношение напряжения на элементах цепи равно отношению сопротивлений на этих элементах; или напряжение на любом элементе последовательной цепи равно произведению E, приложенной к этой цепи, на сопротивление этого элемента, делённому на общее (суммарное) сопротивление всех элементов цепи.
Аналогично можно сформулировать правило делителя тока для параллельной цепи: отношение токов в параллельных ветвях равно отношению проводимостей этих ветвей.
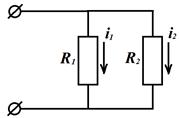
Таким образом,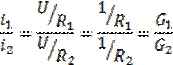 
, и из (12) следует:
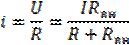; или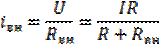 
;
Т.е. ток в одной из двух параллельных ветвей равен произведению тока источника на сопротивление противоположной ветви, делённому на сумму сопротивлений этих ветвей.
Используя правила делителей напряжения и тока, можно осуществить эквивалентные преобразования топологии электрических цепей. Основное условие эквивалентности преобразования одной цепи в другую – сохранение неизменными напряжений и токов в точках преобразования (для пассивных цепей – сопротивлений и проводимостей).
|
|
|
Существуют следующие основные эквивалентные преобразования:
1. Взаимное преобразование реальных источников напряжения и тока (РИН ↔РИТ). Для этого найдём ток нагрузки в последовательной и параллельной схемах, используя (11) и (12):
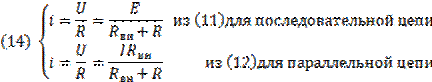
Сопоставляя выражения из (14), можно получить условие эквивалентности для реальных источников напряжения и тока:
.
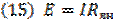При этом идеальные источники напряжения и тока не взаимозаменяемы.
2. Замена нескольких последовательно соединённых элементов одним эквивалентным (если элементы цепи соединены последовательно, то через них протекает один и тот же ток и их сопротивления складываются):
При этом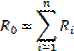 
, где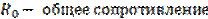 
.
3. Замена нескольких параллельно соединённых сопротивлений (проводимостей) одним эквивалентным (если элементы цепи соединены параллельно, то к ним приложено одно и то же напряжение и их проводимости складываются):
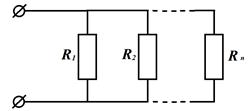
При этом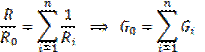 
.
4. Замена нескольких последовательно соединённых источников напряжения (РИН) и их внутренних сопротивлений:
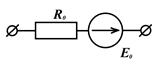
При этом эквивалентные значения будут равны сумме (с учетом направлений ЭДС):
.
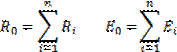5. Замена параллельного соединения нескольких источников тока (РИТ) и их проводимостей одним эквивалентным:
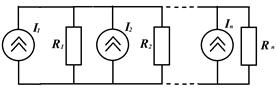
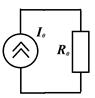
Результирующие значения также будут суммироваться с учетом направлений токов:
.
|
|
|
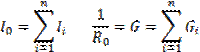6. Замена нескольких параллельно соединённых реальных источников напряжения одним эквивалентным источником тока: сначала сделать замену (1) для каждого РИН 
РИТ, после этого использовать преобразование (5).
7. Замена нескольких последовательно соединённых реальных источников тока одним эквивалентным РИН: сначала замена (1) для каждого РИТ РИН, после этого использовать преобразование (4).
8. Взаимные преобразования треугольника и звезды:
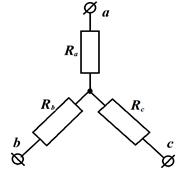
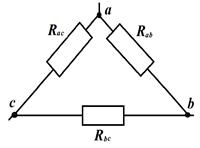
При этом: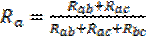 
; 
; 
;
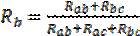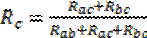И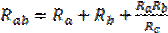 
; 
; 
.
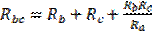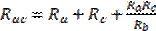Если в узлах «звезды»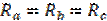 
, то в ветвях «треугольника»:
