2015-04-23
853
Если ряд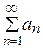 
сходится, то его общий член 
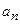стремится к нулю при 
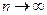, т.е. 
.
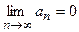Кратко: если ряд сходится, то его общий член стремится к нулю.
Отсюда вытекает достаточный признак расходимости ряда.
Если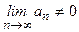 
, то ряд расходится.
Пример 4. Исследовать на сходимость ряд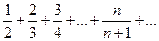 
Для этого ряда общий член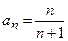 
и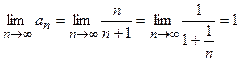 
.
Следовательно, данный ряд расходится.
Пример 5. Исследовать на сходимость ряд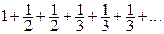 
Очевидно, что общий член этого ряда, вид которого не указан ввиду громоздкости выражения, стремится к нулю при 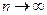, т.е. необходимый признак сходимости ряда выполняется, однако этот ряд расходится, так как его сумма 
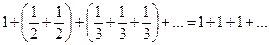стремится к бесконечности.
