Теорема (Первый признак сравнения)
Пусть даны два знакоположительных ряда:
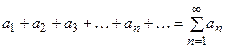 (1)
(1)
и
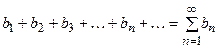 (2)
(2)
причем, начиная с некоторого номера 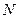 , для любого
, для любого 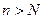 выполняется неравенство
выполняется неравенство 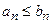 Тогда:
Тогда:
1) из сходимости ряда 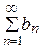 следует сходимость ряда
следует сходимость ряда 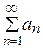 ;
;
2) из расходимости ряда 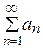 следует расходимость ряда
следует расходимость ряда 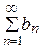 .
.
Схематическая запись первого признака сравнения:
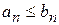
сход.сход.
расх.®расх.
Для применения этого признака часто используют такие ряды-эталоны, сходимость или расходимость которых известна заранее, например:
1) 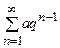 - геометрический (он сходится при
- геометрический (он сходится при 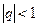 и расходится при
и расходится при 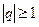 );
);
2) 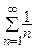 – гармонический (он расходится);
– гармонический (он расходится);
3) 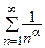 - ряд Дирихле (он сходится при
- ряд Дирихле (он сходится при 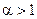 и расходится при
и расходится при 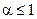 ).
).
Кроме этого часто используют ряды, которые можно получить с помощью следующих очевидных неравенств:
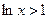
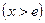 ,
, 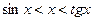
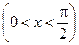 ,
, 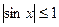 ,
, 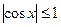
Рассмотрим на конкретном примере схему исследования знакоположительного ряда на сходимость с помощью первого признака сравнения.
Пример 6. Исследовать ряд 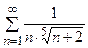 на сходимость.
на сходимость.
Шаг 1. Проверим знакоположительность ряда: 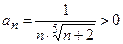 для
для 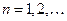
Шаг 2. Проверим выполнение необходимого признака сходимости ряда: 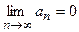 . Так как
. Так как 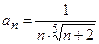 , то
, то 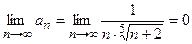 .
.
(Если вычисление предела вызывает трудности, то этот шаг можно пропустить.)
Шаг 3. Используем первый признак сравнения. Для этого подберем для данного ряда ряд-эталон. Так как 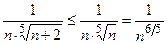 , то в качестве эталона можно взять ряд
, то в качестве эталона можно взять ряд 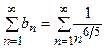 , т.е. ряд Дирихле. Этот ряд сходится, так как показатель степени
, т.е. ряд Дирихле. Этот ряд сходится, так как показатель степени 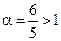 . Следовательно, согласно первому признаку сравнения сходится и исследуемый ряд.
. Следовательно, согласно первому признаку сравнения сходится и исследуемый ряд.
Пример 7. Исследовать ряд 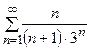 на сходимость.
на сходимость.
1) Данный ряд знакоположительный, так как 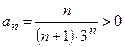 для
для 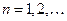
2) Необходимый признак сходимости ряда выполняется, так как
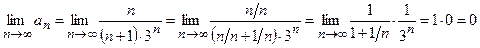
3) Подберем ряд-эталон. Так как 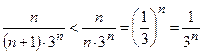 , то в качестве эталона можно взять геометрический ряд
, то в качестве эталона можно взять геометрический ряд 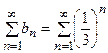
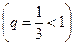 . Этот ряд сходится, следовательно, сходится и исследуемый ряд.
. Этот ряд сходится, следовательно, сходится и исследуемый ряд.
Теорема (Второй признак сравнения)
Если для знакоположительных рядов 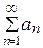 и
и 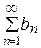 существует отличный от нуля конечный предел
существует отличный от нуля конечный предел 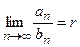 , то ряды сходятся или расходятся одновременно.
, то ряды сходятся или расходятся одновременно.
Замечание. Если 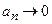 при
при 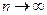 (необходимый признак сходимости), то из условия
(необходимый признак сходимости), то из условия 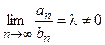 , следует, что
, следует, что 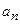 и
и 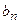 – бесконечно малые одного порядка малости (эквивалентные при
– бесконечно малые одного порядка малости (эквивалентные при 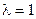 ). Следовательно, если дан ряд
). Следовательно, если дан ряд 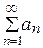 , где
, где 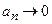 при
при 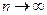 , то для этого ряда можно брать ряд-эталон
, то для этого ряда можно брать ряд-эталон 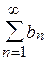 , где общий член
, где общий член 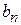 имеет тот же порядок малости, что и общий член данного ряда.
имеет тот же порядок малости, что и общий член данного ряда.
При выборе ряда-эталона можно пользоваться следующей таблицей эквивалентных бесконечно малых при 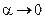 :
:
1) 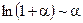 ; 4)
; 4) 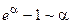 ;
;
2) 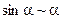 ; 5)
; 5) 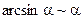 ;
;
3) 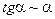 ; 6)
; 6) 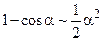 .
.
Пример 8. Исследовать на сходимость ряд 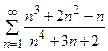 .
.
Данный ряд знакоположительный, так как 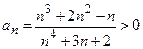 для любого
для любого 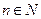 .
.
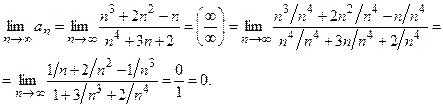
Так как 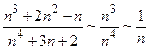 , то возьмем в качестве ряда-эталона гармонический расходящийся ряд
, то возьмем в качестве ряда-эталона гармонический расходящийся ряд 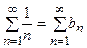 . Поскольку предел отношения общих членов
. Поскольку предел отношения общих членов 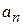 и
и 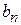 конечен и отличен от нуля (он равен 1), то на основании второго признака сравнения данный ряд расходится.
конечен и отличен от нуля (он равен 1), то на основании второго признака сравнения данный ряд расходится.
Пример 9. Исследовать на сходимость ряд 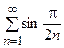 по двум признакам сравнения.
по двум признакам сравнения.
Данный ряд знакоположительный, так как 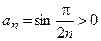 , и
, и 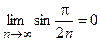 . Поскольку
. Поскольку 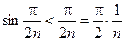 , то в качестве ряда-эталона можно брать гармонический ряд
, то в качестве ряда-эталона можно брать гармонический ряд 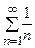 . Этот ряд расходится и следовательно, по первому признаку сравнения, исследуемый ряд также расходится.
. Этот ряд расходится и следовательно, по первому признаку сравнения, исследуемый ряд также расходится.
Так как для данного ряда и ряда-эталона выполняется условие 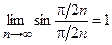 (здесь использован 1-й замечательный предел), то на основании второго признака сравнения ряд
(здесь использован 1-й замечательный предел), то на основании второго признака сравнения ряд 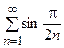 – расходится.
– расходится.
Теорема (Признак Даламбера)
Если для знакоположительного ряда 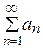 существует конечный предел
существует конечный предел 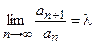 , то ряд сходится при
, то ряд сходится при 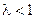 и расходится при
и расходится при 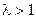 .
.
Замечания:
1) Если 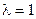 , признак Даламбера не дает ответа на вопрос о сходимости ряда и поэтому необходимо использовать другие признаки сходимости.
, признак Даламбера не дает ответа на вопрос о сходимости ряда и поэтому необходимо использовать другие признаки сходимости.
2) Признак Даламбера дает оценку и остатка ряда. Из неравенства
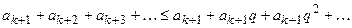 ,
,
следует, что остаток ряда 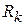
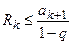 .
.
3) Признак Даламбера удобен на практике тогда, когда общий член ряда содержит показательную функцию или факториал.
Пример 10. Исследовать на сходимость ряд 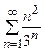 по признаку Даламбера.
по признаку Даламбера.
Данный ряд знакоположительный и 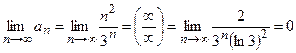 .
.
(Здесь при вычислении дважды применено правило Лопиталя.)
Так как
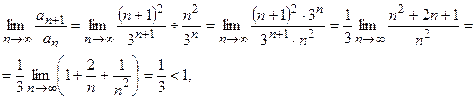
то по признаку Даламбера данный ряд сходится.
Пример 11. Исследовать на сходимость ряд 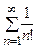 .
.
Данный ряд знакоположительный и 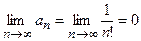 . Поскольку
. Поскольку
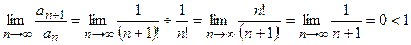 ,
,
то данный ряд сходится.
Теорема (Признак Коши)
Если для знакоположительного ряда 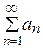 существует конечный предел
существует конечный предел 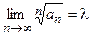 , то при
, то при 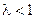 ряд сходится, а при
ряд сходится, а при 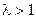 ряд расходится.
ряд расходится.
Замечания:
1) Если 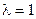 , признак Коши не дает ответа на вопрос о сходимости ряда и поэтому необходимо использовать другие признаки сходимости.
, признак Коши не дает ответа на вопрос о сходимости ряда и поэтому необходимо использовать другие признаки сходимости.
2) Если 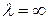 , то ряд расходится.
, то ряд расходится.
Пример 12. Исследовать на сходимость ряд 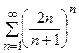 .
.
Данный ряд знакоположительный, так как 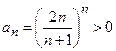 для любого
для любого 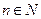 . Поскольку вычисление предела
. Поскольку вычисление предела 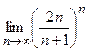 вызывает определенные трудности, то проверку выполнимости необходимого признака сходимости ряда опускаем.
вызывает определенные трудности, то проверку выполнимости необходимого признака сходимости ряда опускаем.
Так как
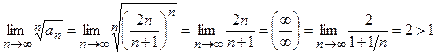 ,
,
то по признаку Коши данный ряд расходится.
Теорема (Интегральный признак сходимости Маклорена — Коши)
Пусть дан ряд
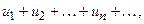
члены которого положительны и не возрастают:
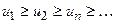
Пусть, далее 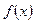 — функция, которая определена для всех вещественных
— функция, которая определена для всех вещественных 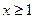 , непрерывна, не возрастает и
, непрерывна, не возрастает и
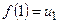 ,
, 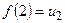 , …,
, …, 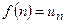 , …
, …
Тогда для сходимости ряда (7) необходимо и достаточно, чтобы сходился (существовал) несобственный интеграл
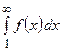 .
.
Пример 13. Исследовать на сходимость ряд 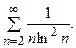
Решение
Члены ряда суть значения функции 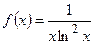 при
при 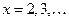 Так как для
Так как для 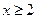
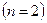 эта функция непрерывна, положительна и убывает, то вопрос о сходимости ряда эквивалентен вопросу о сходимости интеграла
эта функция непрерывна, положительна и убывает, то вопрос о сходимости ряда эквивалентен вопросу о сходимости интеграла 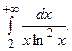 По определению несобственного интеграла
По определению несобственного интеграла
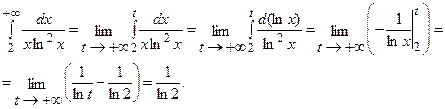
несобственный интеграл сходится, а, следовательно, сходится и исходный числовой ряд.
 2015-04-23
2015-04-23 3163
3163
