Сходящиеся и расходящиеся ряды

Числовые ряды

Числовой ряд. Общий член ряда

Определение. Пусть дана бесконечная последовательность чисел 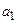, , 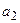,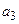..., то выражение вида

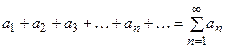(1)

называется числовым рядом, числа 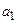, , 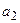,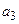...– членами (элементами) ряда, 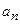– общим членом ряда, если 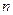не зафиксировано.

Пример1. Дан ряд 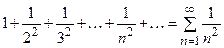,где общий член 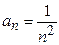. Найти 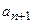. Заменяя в общем члене 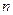на 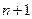, получим .

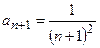Сходящиеся и расходящиеся ряды

Сумма первых n членов ряда (1) называется 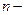ой частичной суммой и обозначается через 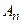. Следовательно, суммы

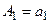– 1-ая частичная сумма;

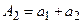– 2-ая частичная сумма;

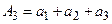– 3-ая частичная сумма;

¼ – ……………………….

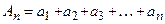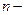– ая частичная сумма;

... – ……………………….

образуют последовательность частичных сумм , ,..., ,...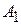

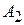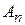Определение Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм, то есть 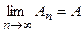. При этом число 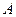называется суммой ряда. Если для данного ряда последовательность частичных сумм 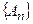не имеет конечного предела при 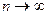, то этот ряд называется расходящимся.

Пример2. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии (геометрический ряд)

, .

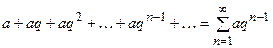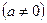Из элементарной математики известно, что сумма n членов геометрической прогрессии 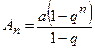. Отсюда следует, что если 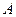, то геометрический ряд сходится и его сумма 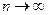. Если же 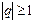, то геометрический ряд расходится.

Пример3. Исследовать на сходимость ряд 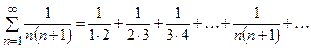.Так как 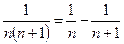, то 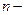ая частичная сумма данного ряда

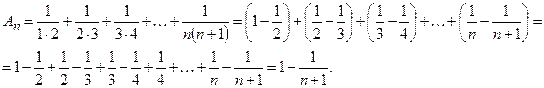
Эта сумма при 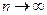имеет предел .

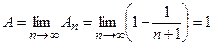Итак, данный ряд сходится и его сумма равна единице.