Преобразование Лапласа и операторный метод анализа

Операторный метод анализа линейных стационарных систем основан на представлении входных и выходных сигналов преобразованиями Лапласа, поэтому кратко вспомним их суть и свойства.

6.10.1 Преобразование Лапласа

Естественным обобщением принципа представления исследуемого сигнала в виде суммы неограниченно большого числа элементарных слагаемых, каждое из которых периодически изменяется во времени по закону exp(jwt), является то, что вместо комплексных экспоненциальных сигналов с чисто мнимыми показателями вводят в рассмотрение экспоненциальные сигналы вида exp(pt), где р = s + jw – полная комплексная частота. Из двух таких комплексных сигналов всегда можно составить вещественный сигнал, например, по следующему правилу: s(t) = 1/2 [exp(pt) + exp(p*t)], где p* = s - jw – комплексно-сопряженная величина. Действительно, при этом:

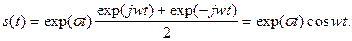
В зависимости от выбора вещественной и мнимой частей комплексной частоты можно получать разнообразные вещественные сигналы. (РИС. СО СТР. 68).

Основные соотношения. Пусть f(t) – некоторый сигнал, вещественный или комплексный, определенный при t > 0 и тождественно равный нулю при отрицательном значении времени. Преобразование Лапласа F(p) этого сигнала задается интегралом:

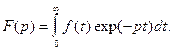(6.34)

Сигнал f(t) называется оригиналом, а функция F(p) – его изображением по Лапласу. Условие существования интеграла (6.34) заключается в следующем: сигнал f(t) должен иметь не более чем экспоненциальную степень роста при t > 0, т.е. должен удовлетворять неравенству ï f(t) ï£ k exp(at), где k, a – положительные числа.

Преобразование Лапласа должно рассматриваться как обобщение преобразования Фурье на случай комплексных частот. По аналогии с последним, зная изображение преобразования Лапласа, можно восстановить оригинал. Для этого в формуле обратного преобразования Фурье 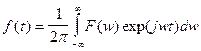следует выполнить аналитическое продолжение, перейдя от мнимой переменной jw к комплексному аргументу (s + jw). На плоскости комплексной частоты интегрирование принято проводить по неограниченно протяженной вертикальной оси; а, поскольку при s = const дифференциал dw = (1/j)dp, то формула обратного преобразования Лапласа приобретает вид:

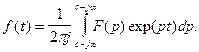(6.35)

Изображения по Лапласу во всех точках комплексной плоскости р, за исключением счетного множества так называемых особых точек, являются аналитическими функциями. Особые точки – как правило, однократные или многократные полюса. На практике широко используют таблицы преобразований Лапласа.

Основные свойства преобразования Лапласа.

1. Линейность: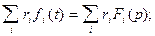

2. Изменение изображения при сдвиге сигнала по временной оси:

f(t - t₀) «exp(-pt₀)F(p) (по аналогии с преобразованием Фурье);

3. Теорема смещения: Если f(t) ¸ F(p), то изображение сигнала, умноженного на экспоненциальную функцию времени, получается путем смещения аргумента изображения: f(t) exp(-at) ¸ F(p + a).

4. Изображение производных от сигнала: Определяется по аналогии с преобразованием Фурье и, в отличие от него, содержит значение самого сигнала в начальной точке: 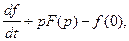и по индукции для производной n-го порядка:

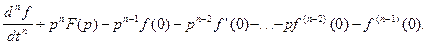
5. Изображение интеграла: Если при t=0 сигнал обращается в нуль, то

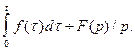
6. Изображение свертки двух сигналов: По аналогии с преобразованием Фурье, свертке двух сигналов отвечает произведение их изображений:

f₁(t)*f₂(t) ¸ F₁(p) F₂(p),

где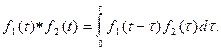

6.10.2 Решение дифференциальных уравнений операторным методом

Пусть дифференциальное уравнение

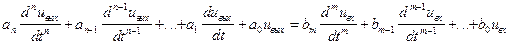(6.36)

устанавливает закон соответствия между сигналами на входе и выходе некоторой линейной стационарной системы. Необходимо ввести ограничение: и_вх(t)=0 при t < 0. Кроме того, логично предположить, что вплоть до момента возникновения входного сигнала система не содержит какой-либо запасенной энергии. Математически это означает, что начальные условия выбраны нулевыми: и_вых(0)=и’_вых(0)=...=и^(n-1)_вых(0)=0. И, наконец, допустим, что область возможных входных сигналов не содержит в себе функций, столь быстро нарастающих во времени, что для них не существует преобразования Лапласа.

Обозначим закон соответствия между оригиналами и изображениями следующим образом: и_вх(t) ¸ U_вх(р); и_вых(t) ¸ U_вых(р).

Вычислив преобразования Лапласа от обеих частей уравнения (6.36), получим:

(a_npⁿ + a_n-1p^n-1 +...+ a₁p + a₀)U_вых(р)=(b_mp^m + b_m-1p^m-1 +...+ b₁p + b₀)U_вх(р). (6.37)

Важнейшей характеристикой, на которой основан операторный метод, является отношение изображений выходного и входного сигналов:

K(p) = U_вых(р)/U_вх(р), (6.38)

называемое передаточной функцией или операторным коэффициентом передачи рассматриваемой системы.

В соответствии с (6.37):

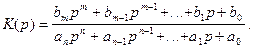(6.39)

В рамках операторного метода передаточная функция является полной математической моделью системы. Если эта функция известна, то поиск выходной реакции системы на заданное входное воздействие разбивается на три этапа:

1. и_вх(t) ® U_вх(р),

2. U_вых(р) = К(р) U_вх(р),

3. U_вых(р) ® и_вых(t).

Кроме своего очевидного преимущества в простоте вычислений перед временным и спектральным методами, операторный метод наиболее удобен для нахождения импульсных и переходных характеристик линейных систем, поскольку изображения по Лапласу для дельта-функции и функции Хевисайда определяются соответственно как

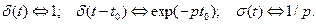
Свойства передаточной функции. Анализ формулы (6.39) показывает, что функция К(р) есть результат аналитического продолжения частотного коэффициента передачи К(jw) с мнимой оси jw на всю плоскость комплексной частоты p = s + jw. Величина К(р) есть функция, аналитическая во всей плоскости р, за исключением конечного числа точек р₁, р₂,..., р_n, являющихся корнями знаменателя в формуле (6.39). Данные точки, т.е. корни уравнения a_npⁿ + a_n-1p^n-1 +...+ a₁p + a₀ = 0, называются полюсами функции К(р). Совокупность точек z₁, z₂,..., z_m, представляющих собой корни уравнения b_mz^m + b_m-1z ^m-1 +...+ b₁z + b₀ = 0, называется нулями передаточной функции.

Вынеся общий множитель К₀, возникающий при делении в (6.39) числителя на знаменатель, можно записать К(р) в так называемом нуль-полюсном представлении, которое является исходным для последующего синтеза четырехполюсников вообще и фильтров в частности:

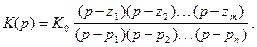
Вещественность коэффициентов дифференциального уравнения (6.37) обеспечивает важную особенность нулей и полюсов – все эти числа либо вещественны, либо образуют комплексно-сопряженные пары.

Формула обращения. Заключительным этапом решения задачи о прохождении сигнала через линейную систему с помощью операторного метода является поиск оригинала, которому отвечает изображение U_вых(р) = К(р) U_вх(р).

Рассмотрим частный случай, когда функция U_вых(р) представляет собой отношение двух многочленов по степени комплексной частоты: U_вых(р)=М(р)/N(p), причем будем считать, что степень числителя m не превосходит степени знаменателя n и, кроме того, корни знаменателя p_i, i = 1, 2,..., n, - простые числа.

Метод, позволяющий находить оригинал, отвечающий такому изображению, основывается на представлении U_вых(р) в виде суммы элементарных дробей:

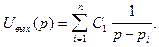
Коэффициенты C_i являются вычетами функции U_вых(р) в точках полюсов, и поэтому

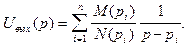
Как известно, изображению 1/(p - p_i) отвечает оригинал exp(p_i t), откуда и следует формула обращения:

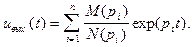(6.40)