Решение. 1)В главном меню SG выбираем раздел H.Distributing Functions и в нем - процедуру Distributing Fitting (сглаживание распределений)

1)В главном меню SG выбираем раздел H.Distributing Functions и в нем - процедуру Distributing Fitting (сглаживание распределений). Появляется экранная форма запроса на сглаживание переменной - табл.2.17.

В этой форме следует заполнить поле «Data vector» (с помощью функциональной клавиши [F7] ввести имя файла и переменной, содержащей данные - D: SIMULA.port1) и поле выбора номера сглаживающей кривой из приведенного в на этом экране списка: «Distribution number». В нашем примере этот номер равен 6 (распределение Пуассона). После этого автоматически будет рассчитано и высвечено на экране статистическое значение параметра выбранного распределения (Mean: 3.87671).

Таблица 2.17

Distribution Fitting

Data vector: D:SIMULA.port1

Distributions available:

(1) Bernoulli (7) Beta (13) Lognormal

(2) Binomial (8) Chi-square (14) Normal

(3) Discrete uniform (9) Erlang (15) Student's t

(4) Geometric (10) Exponential (16) Triangular

(5) Negative binomial (11) F (17) Uniform

(6) Poisson (12) Gamma (18) Weibull

Distribution number: 6

Mean: 3.87671 Histogram

Chi-square test

K-S test

Tail areas

Critical values

Highlight desired entry and press ENTER to select.

1Help 2Edit 3Savscr 4Prtscr 5 6Go 7Vars 8Cmd 9Review 10Quit

INPUT 8/26/98 12:55 STATGRAPHICS Vers. 2.1 DSTFIT

2)В окне выбора исполнительной функции с помощью клавиш управления курсором выбрать «Histogram». На экране появится изображение гистограммы (статистическое распределение) и сглаживающей кривой, построенной для того же значения параметра, что и статистическая величина (т.е. в данном примере: l_теор=3.87671). Эта кривая представляет собой теоретическое распределение - см. рис.2.12. В точках перелома кривой наглядно видны расхождения теоретического и статистического распределения. Предстоит оценить, насколько они существенны.

3)С помощью [F10] вернуться к форме запроса и в окне выбора исполнительной функции показать «Chi-square test». Тем самым для оценки расхождений будет выбран критерий Пирсона (критерий «хи-квад-рат»). Результат выполнения функции «Chi-square test» показан в табл. 2.18. В ней представлена группировочная таблица, описывающая статистическое распределение исходной выборки, и значения вычи-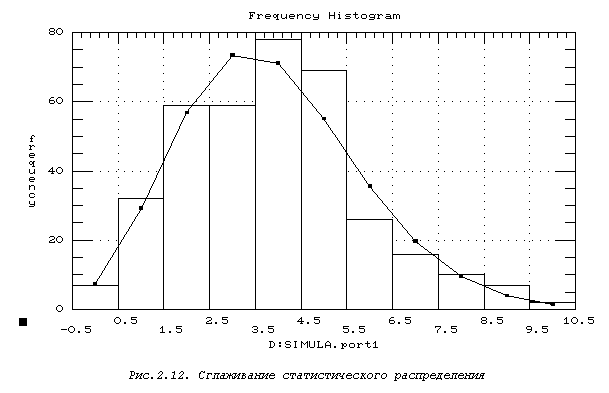

сленных показателей: Chisquare (величина c², рассчитанная по формуле 2.34) и Sig. Level (уровень значимости a). Как видно из таблицы, эти значения равны соответственно 11,5935 и 0,170282.

Таблица 2.18

Chisquare Test

Lower Upper Observed Expected

Limit Limit Frequency Frequency Chisquare

at or below.500 7 8.0418

.500 1.500 32 29.2455

1.500 2.500 59 57.0831

2.500 3.500 59 73 2.8371

3.500 4.500 78 71.6553

4.500 5.500 69 55 3.4603

5.500 6.500 26 36 2.6139

6.500 7.500 16 20.7105

7.500 8.500 10 10.0195

above 8.500 9 7.9264

Chisquare = 11.5935 with 8 d.f. Sig. level = 0.170282

Вероятность p есть обратная вероятность от уровня значимости: p = 1 - a. Для рассматриваемого примера p = 1 - 0,170282» 0,83. Это достаточно большая вероятность, поэтому можно считать, что исходная гипотеза о пуассоновском распределении числа судов, прибывающих в исследуемый порт за сутки, является правдоподобной.

Примечание: в экранной форме табл.2.17 исполнительная функция «K-S test» - проверка выборки по критерию Колмогорова.