Рассмотрим ЛНДУ второго порядка

где 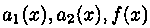 - заданные, непрерывные на (а;b) функции. Уравнение
- заданные, непрерывные на (а;b) функции. Уравнение
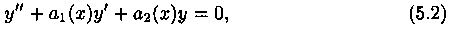
левая часть которого совпадает с левой частью ЛНДУ (5.1), называется соответствующим ему однородным уравнением.
Теорема 5.1 (структура общего решения ЛНДУ). Общим решением у уравнения (5.1) является сумма его произвольного частного решения у* и общего решения 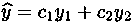 соответствующего однородного уравнения (5.2), т. е.
соответствующего однородного уравнения (5.2), т. е.

Убедимся, что функция (5.3) - решение уравнения (5.1). Так как у* есть решение уравнения (5.1), а 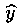 - решение уравнения (5.2), то
- решение уравнения (5.2), то
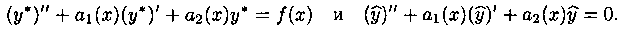
В таком случае имеем:
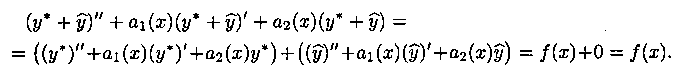
Это означает, что функция 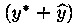 является решением уравнения (5.1).
является решением уравнения (5.1).
Покажем теперь, что функция

является общим решением уравнения (5.1). Для этого надо доказать, что из решения (5.4) можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
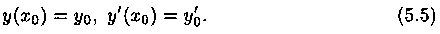
Продифференцировав функцию (5.4) и подставив начальные условия (5.5) в функцию (5.4) и ее производную, получим систему уравнений:
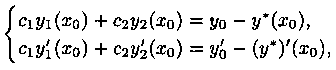
где уо=у(хо), у'0=y'(x0), с неизвестными c1 и с2. Определителем этой системы является определитель Вронского W(x0) для функции y1(x) и у2(х) в точке х=хо. Функции y1(x) и у2(х) линейно независимы (образуют фундаментальную систему решений), т. е. 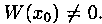 Следовательно, система имеет единственное решение: c1=с01 и с2=с02.
Следовательно, система имеет единственное решение: c1=с01 и с2=с02.
Решение 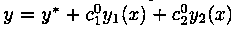 является частным решением уравнения (5.1), удовлетворяющим заданным начальным условиям (5.5). Теорема доказана.
является частным решением уравнения (5.1), удовлетворяющим заданным начальным условиям (5.5). Теорема доказана.
 2015-04-20
2015-04-20 1866
1866
