Замечание

Теорема Ролля есть частный случай теоремы Лагранжа, когда .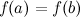

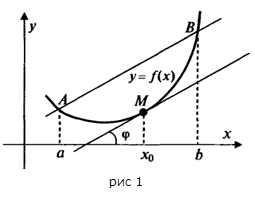
Следствие. (Геометрический смысл теоремы Лагранжа)

На кривой 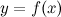между точками и 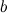найдется точка , такая, что через эту точку можно провести касательную, параллельную хорде 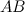(рис. 1).

Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:

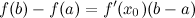
29.) Критерии монотонности функции

Снова рассмотрим функцию y = f (x), считая ее дифференцируемой на некотором интервале (a, b). Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Теорема 1.
Для того, чтобы функция y = f (x) была возрастающей на интервале (a, b), необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале:

f ' (x) ≥ 0 ∀ x ∈ (a, b).

Аналогичный критерий действует для случая функции, убывающей на интервале (a, b):

f ' (x) ≤ 0 ∀ x ∈ (a, b).

Докажем обе части теоремы (необходимость и достаточность) для случая возрастающей функции.

Необходимое условие.
Рассмотрим произвольную точку x ₀ ∈ (a, b). Если функция y = f (x) возрастает на (a, b), то по определению можно записать, что

∀ x ∈ (a, b): x > x ₀ ⇒ f (x) ≥ f (x ₀);

∀ x ∈ (a, b): x < x ₀ ⇒ f (x) ≤ f (x ₀).

Видно, что в обоих случаях выполняется неравенство

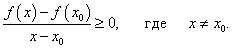
В пределе при x → x ₀ левая часть неравенства равна производной функции в точке x ₀, т.е. по свойству сохранения знака предела:

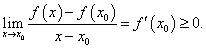
Это соотношение справедливо для любых x ₀ ∈ (a, b).

Рассмотрим достаточное условие, т.е. обратное утверждение.
Пусть производная f ' (x) функции y = f (x) неотрицательна на интервале (a, b):

f ' (x) ≥ 0 ∀ x ∈ (a, b).

Если x ₁ и x ₂ − две произвольные точки данного интервала, такие, что x ₁ < x ₂, то по теореме Лагранжа можно записать:

f (x ₂) − f (x ₁) = f ' (c)(x ₂ − x ₁),

где с ∈ [ x ₁, x ₂] ⇒ c ∈ (a, b).

Поскольку f ' (c) ≥ 0, то правая часть равенства неотрицательна. Следовательно,

f (x ₂) ≥ f (x ₁),

т.е. функция y = f (x) является возрастающей на интервале (a, b).

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая возрастающей функции.

Теорема 2.
Для того, чтобы дифференцируемая на интервале (a, b) функция была строго возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялись следующие условия:

1) f ' (x) ≥ 0 ∀ x ∈ (a, b);

2) f ' (x) тождественно не равно нулю ни в каком промежутке [ x ₁, x ₂] ∈ (a, b).

Условие 1 содержится в теореме 1 и является признаком неубывающей функции. Дополнительное условие 2 требуется для того, чтобы исключить участки постоянства функции, в которых производная f (x) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы 2 следует такая формулировка достаточного признака:

Если для всех x ∈ (a, b) выполняется условие f ' (x) > 0 всюду в интервале (a, b), кроме возможно лишь некоторых отдельных точек, в которых f ' (x) = 0, то функция f (x) является строго возрастающей.

Соответственно, условие f ' (x) < 0 определяет строго убывающую функцию.

Число точек, в которых f ' (x) = 0, является, как правило, конечным. Согласно теореме 2, они не могут плотно заполнять какой-либо промежуток в интервале (a, b).

Приведем также признак возрастания (убывания) функции в точке:

Теорема 3.
Пусть x ₀ ∈ (a, b).

• Если f ' (x ₀) > 0, то функция f (x) строго возрастает в точке x ₀;

• Если f ' (x ₀) < 0, то функция f (x) строго убывает в точке x ₀.

30.) Производные параметрически заданной функции

Предположим, что функциональная зависимость 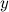от не задана непосредственно 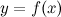, а через промежуточную величину — 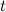. Тогда формулы

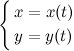
задают параметрическое представление функции одной переменной.

Пусть функция 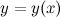задана в параметрической форме, то есть в виде:

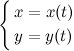
где функци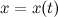и и определены и непрерывны на некотором интервале изменения параметра 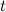. Найдем дифференциалы от правых и левых частей каждого из равенств:

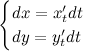
Далее, разделив второе уравнение на первое, и с учетом того, что 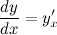, получим выражение для первой производной функции, заданной параметрически:

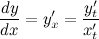
Для нахождения второй производной 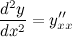выполним следующие преобразования:

31.) Производные неявной функции

Если функция описывается уравнением y = f (x), где переменная y находится в левой части, а правая часть зависит только от аргумента x, то говорят, что функция задана в явном виде. Например, следующие функции заданы явно:

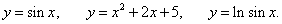
Во многих задачах, однако, функция может быть задана неявным образом, т.е. в виде уравнения

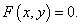
Конечно, любую явную функцию можно записать в неявном виде. Так указанные выше функции можно представить как

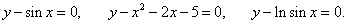
Обратное преобразование можно выполнить далеко не всегда. Часто встречаются функции, заданные неявным уравнением, которые невозможно разрешить относительно переменной y. Например, для приведенных ниже функций

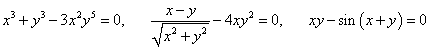
невозможно получить зависимость y (x) в явном виде.

Хорошая новость состоит в том, что для нахождения производной y' (x) неявно заданной функции нет необходимости преобразовывать ее в явную форму. Для этого, зная уравнение F (x, y) = 0, достаточно выполнить следующие действия:

• Сначала необходимо продифференцировать обе части уравнения по переменной x, предполагая,
  что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции. При этом производная нуля (в правой части) также будет равна нулю.
  
  Замечание: Если правая часть отлична от нуля, т.е. неявное уравнение имеет вид

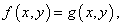
то дифференцируем левую и правую части уравнения.

• Решить полученное уравнение относительно производной y' (x).

Описанный алгоритм нахождения производной неявной функции используется в приведенных ниже примерах.
32.) Исследование поведения функции (область определения, четность, периодичность, первая и вторая производная)

1. Нахождение области определения функции.

Это очень важный шаг исследования функции, так как все дальнейшие действия будут проводиться на области определения.

В нашем примере нужно найти нули знаменателя и исключить их из области действительных чисел.

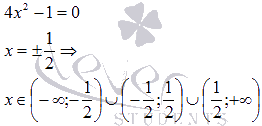
(В других примерах могут быть корни, логарифмы и т.п. Напомним, что в этих случаях область определения ищется следующим образом:
для корня четной степени, например, 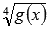- область определения находится из неравенства ;
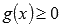для логарифма 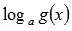- область определения находится из неравенства ).

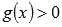Перейти к подробному описанию нахождения области определения функции...

2. Исследование поведения функции на границе области определения, нахождение вертикальных асимптот.

На границах области определения функция имеет вертикальные асимптоты, если односторонние пределы функции в этих граничных точках бесконечны.

В нашем примере граничными точками области определения являются .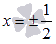

Исследуем поведение функции при приближении к этим точкам слева и справа, для чего найдем односторонние пределы:

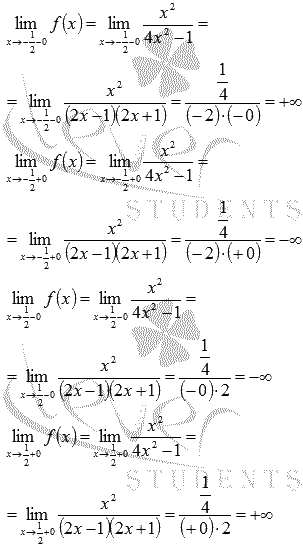
Так как односторонние пределы бесконечны, то прямые 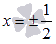являются вертикальными асимптотами графика.

3. Исследование функции на четность или нечетность.

Функция является четной, если 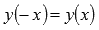. Четность функции указывает на симметрию графика относительно оси ординат.

Функция является нечетной, если 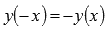. Нечетность функции указывает на симметрию графика относительно начала координат.

Если же ни одно из равенств не выполняется, то перед нами функция общего вида.

В нашем примере выполняется равенство 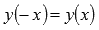, следовательно, наша функция четная. Будем учитывать это при построении графика - он будет симметричен относительно оси oy.

4. Нахождение промежутков возрастания и убывания функции, точек экстремума.

Промежутки возрастания и убывания являются решениями неравенств 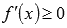и 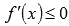соответственно.

Точки, в которых производная обращается в ноль, называют стационарными.

Критическими точками функции называют внутренние точки области определения, в которых производная функции равна нулю или не существует.

ЗАМЕЧАНИЕ (включать ли критические точки в промежутки возрастания и убывания).

o Некоторые авторы полагают, что промежутки возрастания и убывания являются решениями неравенств 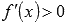и 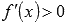. В этом случае критические точки не включаются в промежутки.

o Некоторые авторы полагают, что точки, в которых функция определена, а конечной производной не имеет, нужно включать в промежутки возрастания и убывания (например, функция 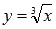в точке х=0 определена, а производная в этой точке бесконечна 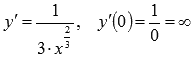, х=0 следует включить в промежуток возрастания функции).

o По нашему мнению, принципиальной важности это не имеет, хотя и может стать причиной разногласий. Чтобы избежать конфликтов, УТОЧНЯЙТЕ У СВОЕГО ПРЕПОДАВАТЕЛЯ ЕГО ОТНОШЕНИЕ К ВКЛЮЧЕНИЮ КРИТИЧЕСКИХ ТОЧЕК В ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ. А еще лучше, ссылайтесь на математическую литературу, рекомендованную министерством образования РФ.

Мы будем включать критические точки в промежутки возрастания и убывания, если они принадлежат области определения функции.

Таким образом, чтобы определить промежутки возрастания и убывания функции

o во-первых, находим производную;

o во-вторых, находим критические точки;

o в-третьих, разбиваем область определения критическими точками на интервалы;

o в-четвертых, определяем знак производной на каждом из промежутков. Знак «плюс» будет соответствовать промежутку возрастания, знак «минус» - промежутку убывания.

33.) Функции нескольких переменных Частные произведения. Градиент.

Частной производной функции z=f(x,y) по аргументу x называется предел отношения частного приращения функции к соответствующему приращению аргумента Dx, когда DxÞ0.

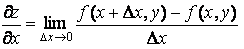, (2-115)

аналогично и по переменной y

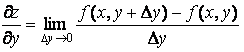, (2-116)

кроме того, частные производные могут обозначаться как:

.

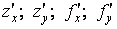При вычислении частных производных по одной из переменных вторая переменная считается постоянной.

Пример 1

z=x²× sin (y) Þ 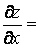2x× sin (y). 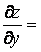x²× cos (x).

Пример 2.

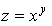) Þ ; .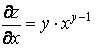

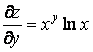Замечание:

частные производные могут вычисляться для всех независимых переменных функции нескольких переменных.

Можно предположить, что функции, получаемые в результате дифференцирования по одной из переменных, тоже будут являться функциями нескольких переменных.

Определение: частная производная от частной производной функции называется частной производной второго порядка.

Таких частных производных второго порядка для функции двух переменных будет уже четыре:

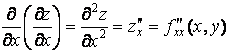. Функция два раза подряд дифференцируется по x;

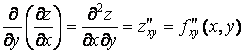(2-117)

здесь дифференцируется сначала по x затем по y;

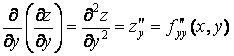(2-118)

функция два раза подряд дифференцируема по y;

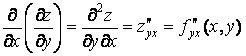(2-119)

функция дифференцируема сначала по y, затем по x.

Частные производные находят по правилам и формулам, аналогично формулам для обычных производных. Надо только помнить, по какой производной проводится дифференцирование, считать эту величину изменяющейся, а остальные - постоянными.

Пример.

Найти частные производные второго порядка от функции

z=x³·y²+2·y-6·x+1 Þ z’_x=3x²y²-6; z^’_y=2x³y+2; z”_xx =6xy²; =6x²y; z^”_yy=2x³; z^”_yx=6x²y.

Как видим, 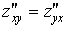. Таково общее свойство смешанных производных.

ГРАДИЕНТ ФУНКЦИИ

и = f(x, у, z), заданной в некоторой обл. пространства (X Y Z), есть вектор с проекциями 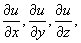обозначаемый символами: grad 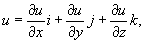где i, j, k — координатные орты. Г. ф. — есть функцияточки (х, у, z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигаетнаибольшего значения и равна: 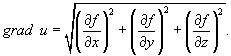Направление градиента естьнаправление наибыстрейшего возрастания функции. Г. ф. в данной точке перпендикулярен поверхностиуровня, проходящей через эту точку. Эффективность использования Г. ф. при литологических исследованияхбыла показана при изучении эоловых отл. Центральных Каракумов.

34.) Производные высших порядков. (Формула Лейбница)

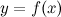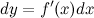Пусть функция зависит от переменной и дифференцируема в точке . Может оказаться, что в точке дифференциал , рассматриваемый как функция от , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала 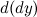данной функции, который называется дифференциалом второго порядка функции 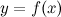. Дифференциал второго порядка обозначается следующим образом:

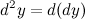
Аналогично определяются дифференциалы более высоких порядков.