Пусть в области 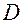 задана функция двух переменных
задана функция двух переменных 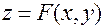 .
.
Определение. Функция 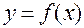 в окрестности
в окрестности 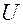 точки
точки 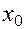 , задана неявно уравнением
, задана неявно уравнением
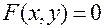 , (20)
, (20)
если при всех 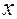 из этой окрестности справедливо равенство
из этой окрестности справедливо равенство 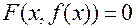 .
.
Заметим, что обычное, «явное» задание функции можно рассматривать как частный случай неявного задания: 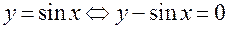 ; здесь
; здесь 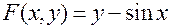 .
.
Теорема. Пусть для неявной функции 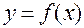 , задаваемой уравнением
, задаваемой уравнением 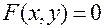 , имеем
, имеем 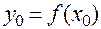 , так что
, так что
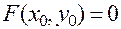 , (21)
, (21)
и выполняются три условия:
1. Неявная функция 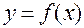 непрерывна в точке
непрерывна в точке 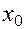 .
.
2. Функция 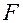 и ее частные производные
и ее частные производные 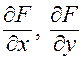 непрерывны в точке
непрерывны в точке 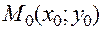 .
.
3. 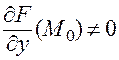 .
.
Тогда неявная функция 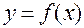 дифференцируема в точке
дифференцируема в точке 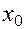 , и
, и
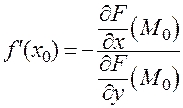 .
.
Доказательство. Придадим переменной 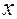 в точке
в точке 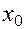 приращение
приращение 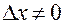 ; оно, в свою очередь, вызовет приращение
; оно, в свою очередь, вызовет приращение 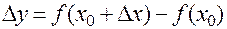 неявной функции, и, как следствие, полное приращение функции
неявной функции, и, как следствие, полное приращение функции 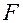 :
:
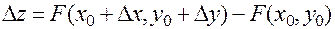 .
.
Пара чисел 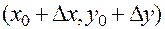 , будучи аргументом и значением неявной функции, также удовлетворяет уравнению (20), то есть
, будучи аргументом и значением неявной функции, также удовлетворяет уравнению (20), то есть
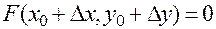 . (22)
. (22)
При этом в силу непрерывности функции 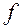 имеем:
имеем: 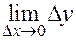 =0.
=0.
Теперь, с одной стороны, из (21) и (22) следует
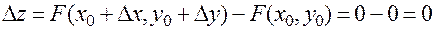 ,
,
а с другой стороны, ввиду непрерывности частных производных, для 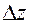 имеет место представление (4):
имеет место представление (4):
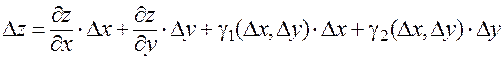
с бесконечно малыми 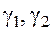 при
при 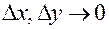 . Таким образом,
. Таким образом,
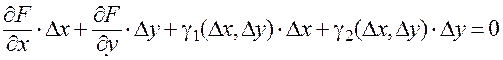 .
.
Выразим отсюда 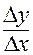 :
:
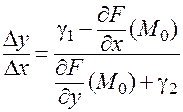
(знаменатель в правой части отличен от нуля в малой окрестности точки  ввиду условий
ввиду условий 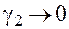 и
и 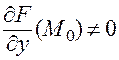 ). Переходя в этом равенстве к пределу при
). Переходя в этом равенстве к пределу при 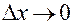 , получаем:
, получаем:
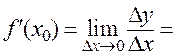
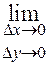
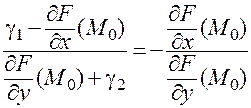 .
.
Пример. Пусть неявная функция задана уравнением
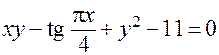 ;
;
здесь 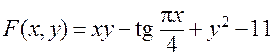 . Точка
. Точка 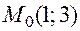 удовлетворяет уравнению, так что для неявной функции
удовлетворяет уравнению, так что для неявной функции 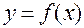 имеем:
имеем: 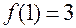 . Далее,
. Далее,
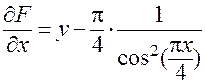 ;
; 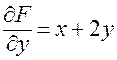 .
.
Поэтому
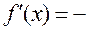
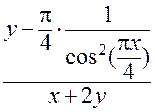 .
.
и 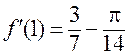 .
.
 2015-05-14
2015-05-14 1872
1872
