Пусть дана таблица значений
| х | х1 | х2 | х3 | ............ | хп |
| у | у1 | у2 | у3 | ............ | уп |
Требуется составить полином (функцию) y = f (x) степени m ≤ n – 1, который принимал бы заданные значения yi при соответствующих значениях xi: yi = f (xi) (i = 1, 2, 3, ………n). Иными словами график функции должен проходить через заданные точки M (xi; yi)
Данная задача выполнима при использовании интерполяционного полинома Лагранжа:
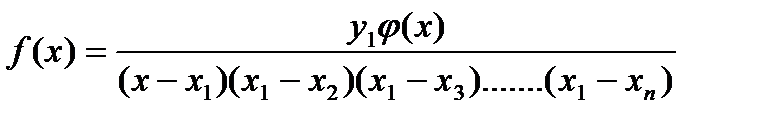 +
+
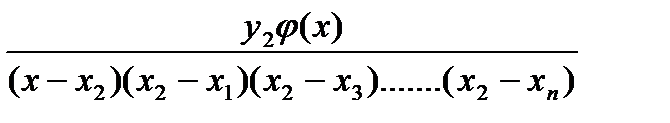 +......
+......
....+ 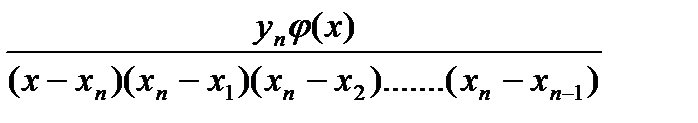 (1)
(1)
или
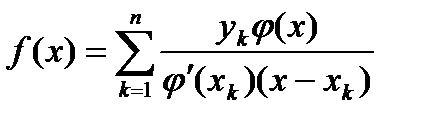 (2)
(2)
где 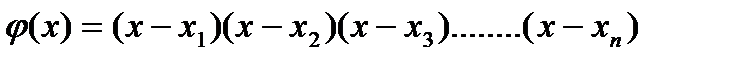 - вспомогательная функция п -й степени, в которой xi – заданные табличные значения аргумента.
- вспомогательная функция п -й степени, в которой xi – заданные табличные значения аргумента.
Пример 2.1
Составить полином Лагранжа, удовлетворяющий таблице значений
| х | ||||
| у |
 2015-05-14
2015-05-14 455
455








