Физический смысл второй производной

Физический смысл производной второго порядка проясняется из того, что если первая производная f’(x) задаёт мгновенную скорость изменения значений f(x) в момент времени x в момент времени f’(x), задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений f(x).

Следовательно, третья производная - это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения,

.

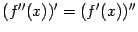7. Промежутки монотонности. Экстремумы функции.

Определение. Функция 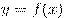называется возрастающей на множестве 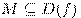, если для любых значений аргумента 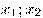из 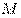выполняется условие .

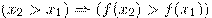Теорема 1. Если функция 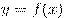имеет положительную (отрицательную) производную в каждой точке промежутка 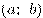, то 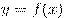возрастает (убывает) на этом промежутке.

Теорема 2. Если функция непрерывна на промежутке 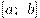и возрастает (убывает) на промежутке 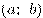, то она возрастает (убывает) и на промежутке .

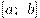Промежутки, на которых функция 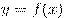возрастает (убывает) называются промежутками монотонности функции .

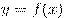Замечание. Функция возрастающая (убывающая) на всей области определения называется возрастающей (убывающей) функцией.

Замечание. Функция, возрастающая (убывающая) на каждом из нескольких промежутках не обязательно убывает на их объединении.

Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

8. Наибольшее и наименьшее значение функции.

Наибольшим значением функции y=f(x) на промежутке X называют такое значение 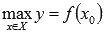, что для любого 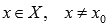справедливо неравенство .

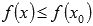Наименьшим значением функции y=f(x) на промежутке X называют такое значение 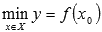, что для любого 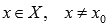справедливо неравенство .

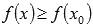9. Исследование функции с помощью производной.

1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢(x) ³ 0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f¢(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Определение. Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функцияf(x) имеет в точке х₂ минимум, если f(x₂ +Dx) > f(x₂) при любом Dх (Dх может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

Определение. Точки максимума и минимума функции называются точками экстремума.

Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

10.Неопределённый интеграл и его свойства. Метод непосредственного интегрирования.