Вторая производная

Всё очень просто. Вторая производная – это производная от первой производной: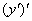

Стандартные обозначения второй производно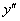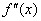й: , или 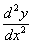(дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите 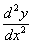функции…». А студент сидит и битый час чешет репу, что это вообще такое.

Рассмотрим простейший пример. Найдем вторую производную от функции .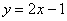

Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:

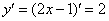
Теперь находим вторую производную:

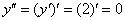
Готово.

Рассмотрим более содержательные примеры.

Пример 11

Найти вторую производную функции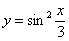

Найдем первую производную:

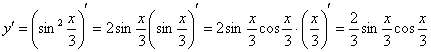
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу 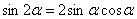. Точнее говоря, использовать формулу будем в обратном направлении: :

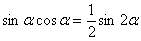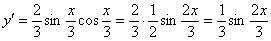
Находим вторую производную:

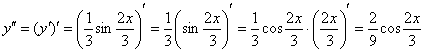
Готово.

Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу :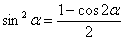

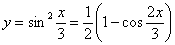
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.

Отмечу, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.

Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.

Например: Вычислим значение найденной второй производной в точке :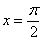

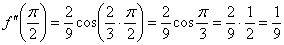
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы.

Пример 12

Найти вторую производную функции 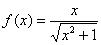. Найти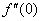

Это пример для самостоятельного решения.

Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но встречаются значительно реже. Можно рассказать о специфических приемах, формуле Лагранжа, и по мере наличия времени я обязательно напишу отдельный методический материал.

Желаю успехов!

Решения и ответы:

Пример 2: Найдем производную:

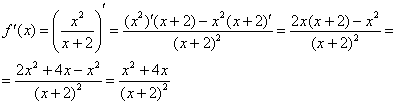
Вычислим значение функции в точке :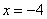

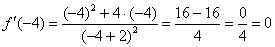
Пример 4: Найдем производную:

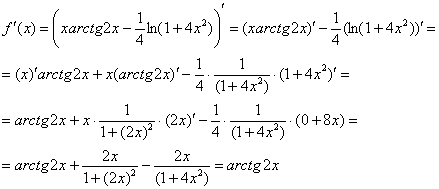
Вычислим производную в заданной точке:

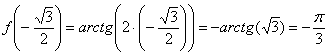
П ример 6: Уравнение касательной составим по формуле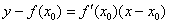
1) Вычислим значение функции в точке :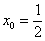

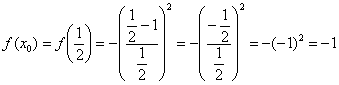
2) Найдем производную. Перед дифференцированием функцию выгодно упростить:


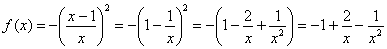
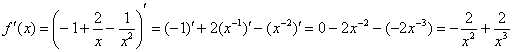
3) Вычислим значение производной в точке :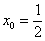

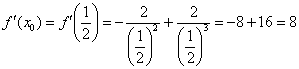
4) Подставим значени я 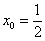, 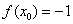и 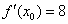в формулу :

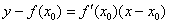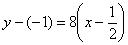
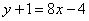
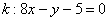
Пример 8: Преобразуем функцию:

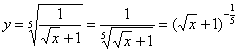
Найдем производную:

Запишем дифференциал:

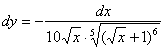
Пример 10: Найдем производную:

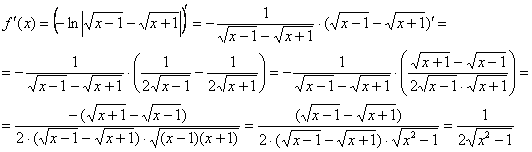
Запишем дифференциал:

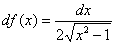
Вычислим дифференциал в точке :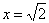

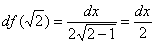
Пример 12: Найдем первую производную:

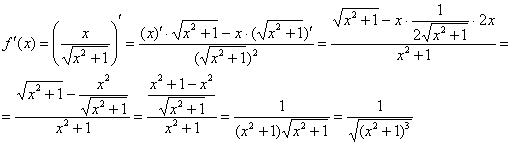
Найдем вторую производную:

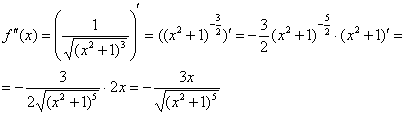
Вычислим: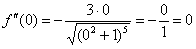

Автор: Емелин Александр

Производная по определению (через предел). Примеры решений

Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на свет таблицы производных и правил дифференцирования. Начало положено в статье о смысле производной, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме.

Этот же урок носит ярко выраженную практическую направленность, более того, рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий: Как найти производную? и Производная сложной функции.

Но без чего-чего сейчас точно не обойтись, так это без пределов функций. Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, что производная функции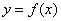 в точке 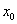задаётся формулой:

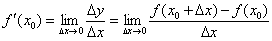
Напоминаю обозначения и термины:
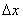называют приращением аргумента;
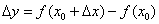– приращением функции;
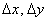– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).

Очевидно, что 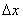является «динамической» переменной, 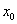– константой и результат вычисления предела 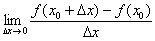– ЧИСЛОМ. И в самом деле, ведь производная в точке 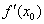– это число (см. практикум Простейшие задачи дифференцирования).

В качестве точки 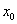можно рассмотреть ЛЮБОЕ значение 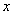, принадлежащее области определения функции 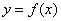, в котором существует производная.

! Примечание: оговорка «в котором существует производная» – в общем случае существенна! Так, например, точка 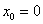хоть и входит в область определения функции 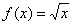, но производной 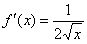там не существует. Поэтому формула 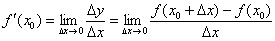не применима в точке 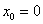, и укороченная формулировка без оговорки будет некорректна. Это же замечание следует делать для некоторых других функций с «обрывами» графика, в частности, для арксинуса, арккосинуса, а также у функций, графики которых содержат «плохие» остриё и изломы. Данные моменты подробнее разъясняются в статье Интервалы монотонности и экстремумы функции.

Таким образом, после замены 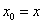, получаем вторую рабочую формулу:

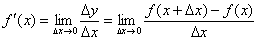
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение 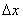. Результатом вычисления предела 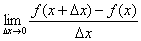является производная функция .

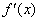Исходя из вышесказанного, сформулируем условия двух типовых задач:

– Найти производную в точке, используя определение производной.

– Найти производную функцию, используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.

Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число, а во втором – функцию.