Задача №8. Найти наименьшее целое решение неравенства

Найти наименьшее целое решение неравенства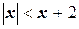

Решение

1. Пусть . (*)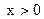

Тогда исходное неравенство принимает вид:

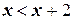или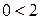

Последнее неравенство верно для всех 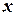, а с учетом условия (*) получаем:

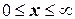
2. Пусть . (**)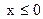

Тогда исходное неравенство принимает вид:

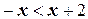или ,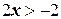

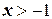
С учетом условия (**) получаем:

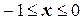
Объединив полученные решения, найдём решение исходного неравенства: 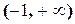. Наименьшим целым числом, принадлежащим этому интервалу, является .

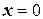Ответ: 0.

Задача №9

Найти 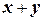, если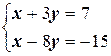

Решение

Вычитая из первого уравнения системы второе, получим уравнение:

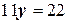
Следовательно , .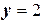

.

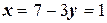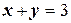Ответ: 3.