1. Определённый интеграл – это число! Его значение зависит только от вида функции 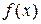 и пределов интегрирования, но не от переменной интегрирования, которую можно обозначать любой буквой:
и пределов интегрирования, но не от переменной интегрирования, которую можно обозначать любой буквой:
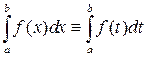 .
.
Интеграл 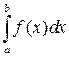 был введен в предположении, что
был введен в предположении, что 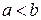 . Обобщим понятие определенного интеграла на случай, когда
. Обобщим понятие определенного интеграла на случай, когда 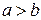 и
и 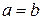 .
.
2. 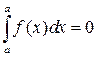 . 3.
. 3. 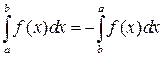
Рассмотрим свойства определённого интеграла, которые имеют аналоги в случае интеграла неопределённого.
4. Если 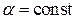 , то
, то 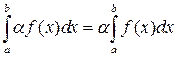 .
.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: 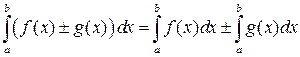 .
.
Перейдем теперь к свойствам определённого интеграла, которые не имеют аналогов в случае неопределённого интеграла.
6. Если отрезок интегрирования разбит на части, то интеграл на всём отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых 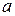 ,
, 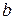 ,
, 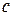 .
.
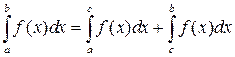 .
.
7. Если 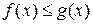 на отрезке
на отрезке 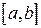 , то
, то 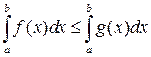 .
.
8. Пусть на отрезке 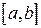 , где
, где 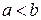 ,
, 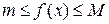 . Тогда
. Тогда
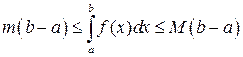 .
.
9. Теорема о среднем. Если функция 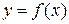 непрерывна на отрезке
непрерывна на отрезке 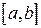 , то найдется такое число
, то найдется такое число 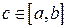 , что
, что
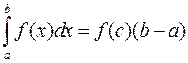 .
.
10. Если функция 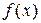 интегрируема на отрезке
интегрируема на отрезке 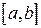 , то функция
, то функция 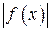 также интегрируема на отрезке
также интегрируема на отрезке 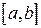 и имеет место неравенство
и имеет место неравенство
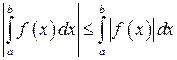
 2015-05-14
2015-05-14 294
294








