Геометрический смысл определенного интеграла

Понятие определенного интеграла введено таким образом, что в случае, когда функция 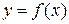неотрицательна на отрезк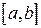е , где 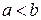, 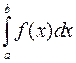численно равен площади 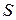под кривой 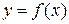на .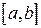

Учитывая сказанное, мы можем указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,

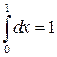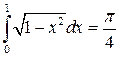, , и т.д.

(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса.)