Пусть в полярной системе координат задана функция 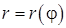 , где
, где 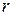 – полярный радиус,
– полярный радиус, 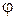 – полярный угол. Пусть, далее, функция
– полярный угол. Пусть, далее, функция 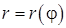 непрерывна при изменении угла
непрерывна при изменении угла 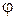 в пределах
в пределах 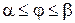 (
(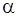 и
и 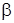 – в радианах). Фигура, ограниченная линией
– в радианах). Фигура, ограниченная линией 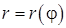 , с которой любой луч, исходящий из полюса
, с которой любой луч, исходящий из полюса 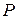 , пересекается не более чем в одной точке, и двумя лучами
, пересекается не более чем в одной точке, и двумя лучами 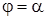 и
и 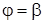 , называется криволинейным сектором.
, называется криволинейным сектором.
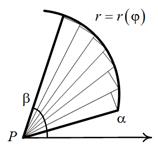 |
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением 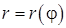 и двумя полярными радиусами
и двумя полярными радиусами 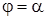 и
и 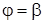 (
(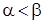 ), находится по формуле
), находится по формуле
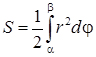 .
.
Пример 7. Вычислить площадь фигуры, ограниченной кривой 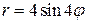 .
.
Решение. Найдем область определения угла 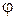 из условия, что
из условия, что 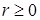 . Имеем:
. Имеем: 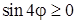 , т. е.
, т. е.
 .
.
Соответственно величина угла 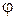 меняется в следующих пределах:
меняется в следующих пределах:
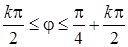
в зависимости от значения 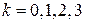 . Найдем границы изменения величины угла
. Найдем границы изменения величины угла 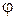 :
:
при 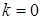 : : | 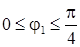 ; ; |
при 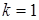 : : | 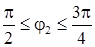 ; ; |
при 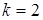 : : | 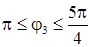 ; ; |
при 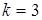 | 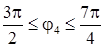 |
где 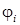 – область определения
– область определения 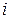 -го лепестка.
-го лепестка.
Достаточно вычислить площадь одного лепестка
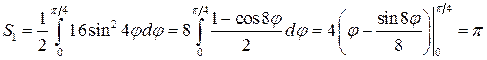
Следовательно, площадь всех лепестков 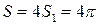
 2015-05-14
2015-05-14 5414
5414