2015-05-18
738
Приводимая ниже таблица 5.1 содержит ежегодные данные о следующих показателях экономики Франции за период с 1949 по 1960 годы (млрд. франков, в ценах 1959 г.):
Y –объем импорта товаров и услуг во Францию;
X 1 –валовой национальный продукт;
X 2 –потребление семей.
Таблица 5.1
| год | Y | X 1 | X 2 | год | Y | X 1 | X 2 |
| 15.9 | 149.3 | 4.2 | 22.7 | 202.1 | 2.1 | ||
| 16.4 | 161.2 | 4.1 | 26.5 | 212.4 | 5.6 | ||
| 19.0 | 171.5 | 3.1 | 28.1 | 226.1 | 5.0 | ||
| 19.1 | 175.5 | 3.1 | 27.6 | 231.9 | 5.1 | ||
| 18.8 | 180.8 | 1.1 | 26.3 | 0.7 | |||
| 20.4 | 190.7 | 2.2 | 31.1 | 5.6 |
Выберем модель наблюдений в виде
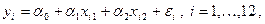
где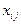 
– значение показателя 
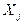в i- м наблюдении (i- му наблюдению соответствует 
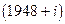год. Будем, как обычно, предполагать что 
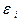нормально распределенные случайные величины с параметрами 
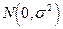и что значение 
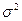нам не известно. Регрессионный анализ дает следующие результаты: 
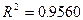и
| Переменная | Коэф-т | Ст. ошибка | t-статист. | P-знач. |
| –8.570 | 2.869 | -2.988 | 0.0153 | |
| X1 | 0.029 | 0.110 | 0.267 | 0.7953 |
| X2 | 0.177 | 0.166 | 1.067 | 0.3136 |
Обращают на себя внимание выделенные курсивом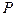 
-значения. В соответствии с ними, проверка каждой отдельной гипотезы 
, 
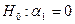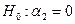(даже при уровне значимости 
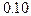) приводит к решению о ее неотклонении. Соответственно, при реализации каждой из этих двух процедур проверки соответствующий параметр 
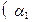или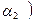 
признается статистически незначимым. И это выглядит противоречащим весьма высокому значению коэффициента детерминации.
По-существу, вопрос стоит таким образом: необходимо построить статистическую процедуру для проверки гипотезы
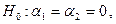
конкретизирующей значения не какого-то одного, а сразу двух коэффициентов.
И вообще, как проверить гипотезу
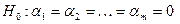
(гипотеза значимости регрессии) в рамках нормальной линейной модели множественной регрессии
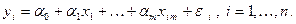
Соответствующий статистический критерий основывается на так называемой F-статистике
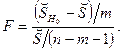
Здесь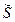 
– остаточная сумма квадратов, получаемая при оценивании полной модели (с 
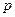объясняющими переменными, включая тождественную единицу), а 
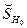– остаточная сумма квадратов, получаемая при оценивании модели с наложенными гипотезой 
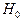ограничениями на параметры. Но последняя (редуцированная) модель имеет вид
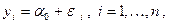
и применение к ней метода наименьших квадратов приводит к оценке
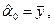
так что
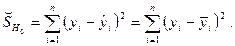
Следовательно,
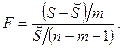
В некоторых пакетах статистического анализа (например, в EXCEL) в распечатках результатов приводятся значения числителя и знаменателя этой статистики (в графе Средние квадраты – Mean Squares).
Если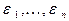 
нормально распределенные случайные величины с параметрами 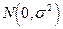, то указанная 
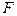-статистика, рассматриваемая как случайная величина, имеет при гипотезе H 0 (т. е. когда действительно α 1 =¼= αm= 0) стандартное распределение 
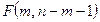, называемое F-распределением Фишера с m и (n-m- 1) степенями свободы.
Чем больше отношение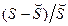 
, тем больше есть оснований говорить о том, что совокупность переменных 
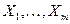действительно помогает в объяснении изменчивости объясняемой переменной 
.
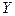В соответствии с этим, гипотеза
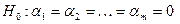
отвергается при «слишком больших» значениях F, скорее указывающих на невыполнение этой гипотезы. Соответствующее пороговое значение определяется как квантиль уровня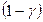 
распределения 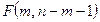, обозначаемая символом 
.
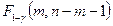Итак, гипотеза Н 0 отвергается, если выполняется неравенство
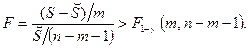
При этом вероятность ошибочного отвержения гипотезы 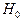равна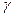 
.
Статистические пакеты, выполняющие регрессионный анализ, приводят среди прочих результатов такого анализа также значение 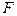указанной 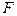-статистики и соответствующее ему P-значение (P-value), т. е. вероятность
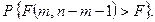
В частности, в рассмотренном выше примере с импортом товаров и услуг во Францию вычисленное (наблюдаемое) значение 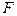-статистики равно 
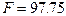, в то время как критическое значение
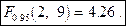
Соответственно, -значение крайне мало – в распечатке результатов приведено значение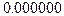 
. Значит, здесь нет практически никаких оснований принимать составную гипотезу 
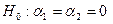, хотя каждая из частных гипотез
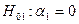и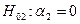 
,
рассматриваемая сама по себе, в отрыве от второй, не отвергается.
Подобное положение встречается не так уж и редко и связано с проблемой мультиколлинеарности данных. Далее мы уделим этой проблеме определенное внимание.
Пример 5.5. Анализ данныхоб уровнях безработицы среди белого и цветного населения США приводит к следующим результатам:
, 
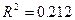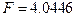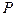, -значение = 
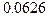, так что при выборе 
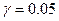гипотеза 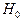не отвергается, а при выборе 
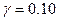отвергается.
Пример 5.6. Анализ зависимости спроса на куриные яйца от цены приводит к значениям
, 
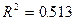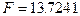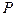, -значение = 
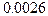, так что гипотеза 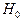отвергается, а регрессия признается статистически значимой.
Пример 5.7. Зависимость производства электроэнергии в США от мирового рекорда по прыжкам в высоту с шестом:
, 
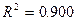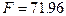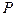, -значение = 
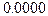, регрессия признается статистически значимой.
Пример 5.8. Потребление свинины в США в зависимости от оптовых цен:
, 
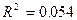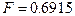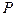, -значение = 
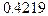, так что гипотеза 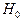не отвергается даже при выборе .
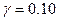Отметим, наконец, еще одно обстоятельство. Во всех четырех рассмотренных примерах регрессионного анализа модели простой (парной) линейной регрессии (m= 1 ) вычисленные 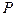-значения 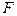-статистик совпадают с 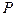-значениями 
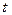-статистик, используемых для проверки гипотезы 
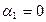. Факт такого совпадения отнюдь не случаен и может быть доказан с использованием алгебраических преобразований.
Применение критериев, основанных на статистиках, имеющих при нулевой гипотезе 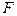-распределение Фишера (F-критерии), отнюдь не ограничивается только что рассмотренным анализом статистической значимости регрессии. Такие критерии широко применяются в процессе подбора модели.
Пусть мы находимся в рамках множественной линейной модели регрессии
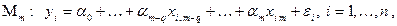
c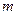 
объясняющими переменными, и гипотеза 
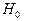состоит в том, что в модели 
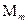последние 
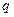коэффициентов равны нулю, т. е.
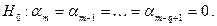
Тогда при гипотезе 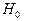(т. е. в случае, когда она верна) мы имеем редуцированную модель
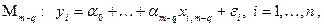
уже с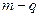 
объясняющими переменными.
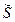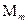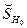Пусть - остаточная сумма квадратов в полной модели , а – остаточная сумма квадратов в редуцированной модели 
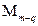. Если гипотеза 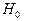верна и выполнены стандартные предположения о модели (в частности, 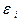нормально распределенные случайные величины с параметрами 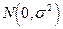), то тогда F- статистика
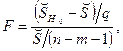
рассматриваемая как случайная величина, имеет при гипотезе H 0 (т. е. когда действительно αm = αm- 1 = ¼= αm-q+ 1 = 0) F-распределение Фишера F (q, n-m- 1) с q и (n-m- 1) степенями свободы.
F-статистика измеряет, в соответствующем масштабе, возрастание объясненной суммы квадратов вследствие включения в модель дополнительного количества объясняющих переменных.
Естественно считать, что включение дополнительных переменных существенно, если указанное возрастание объясненной суммы квадратов достаточно велико. Это приводит нас к критерию проверки гипотезы
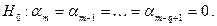
основанному на F-статистике и отвергающему гипотезу 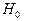, когда наблюдаемое значение 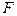этой статистики удовлетворяет неравенству
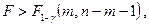
где 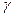– выбранный уровень значимости критерия (вероятность ошибки 1-го рода).
Пример 5.9. В таблице 5.2. приведены данные по США о следующих макроэкономических показателях:
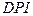–годовой совокупный располагаемый личный доход;
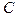–годовые совокупные потребительские расходы;
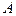–финансовые активы населения на начало календарного года
(все показатели указаны в млрд. долларов, в ценах 1996 г.).
Таблица 5.2
| год | C | DPI | A |
| 1300.5 | 1433.0 | 1641.6 | |
| 1339.4 | 1494.9 | 1675.2 | |
| 1405.9 | 1551.1 | 1772.6 | |
| 1458.3 | 1601.7 | 1854.7 | |
| 1491.8 | 1668.1 | 1862.2 | |
| 1540.3 | 1730.1 | 1902.8 | |
| 1622.3 | 1797.9 | 2011.4 | |
| 1687.9 | 1914.9 | 2190.6 | |
| 1672.4 | 1894.9 | 2301.8 | |
| 1710.8 | 1930.4 | 2279.6 | |
| 1804.0 | 2001.0 | 2308.4 |
Рассмотрим модель наблюдений
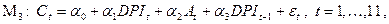
где индексу 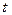соответствует 
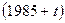год. Это модель с 3 объясняющими переменными:
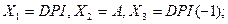
символ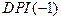 
обозначает переменную, значения которой запаздывают на одну единицу времени относительно значений переменной, 
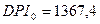. Оценивание этой модели дает следующие результаты:
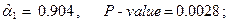
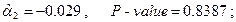
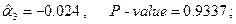
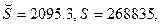
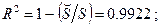
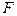— статистика критерия проверки значимости регрессии в целом
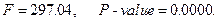
Регрессия имеет очень высокую статистическую значимость. Вместе с тем, каждый из коэффициентов при двух последних переменных статистически незначим, так что, в частности, не следует придавать особого значения отрицательности оценок этих коэффициентов.
Используя – критерий, мы могли бы попробовать удалить из модели какую-нибудь одну из двух последних переменных, и если оставшиеся переменные окажутся значимыми, то остановиться на модели с 2 объясняющими переменными; если же и в новой модели окажутся статистически незначимые переменные, то произвести еще одну редукцию модели.
Рассмотрим, в этой связи, модель
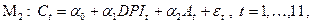
с удаленной переменной . Для нее получаем:
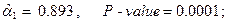
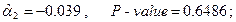
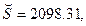
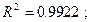
F- статистика критерия проверки значимости регрессии в этой модели
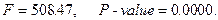
Поскольку здесь остается статистически незначимым коэффициент при переменной 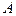, можно произвести дальнейшую редукцию, переходя к модели
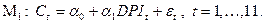
Для этой модели
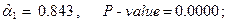
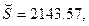
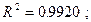
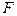-статистика критерия проверки значимости регрессии в этой модели
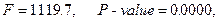
и эту модель в данном контексте можно принять за окончательную.
С другой стороны, обнаружив при анализе модели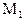 
(посредством применения t-критериев) статистическую незначимость коэффициентов при двух последних переменных, мы можем попробовать выяснить возможность одновременного исключения из этой модели указанных объясняющих переменных, опираясь на использование соответствующего F-критерия.
Исключение двух последних переменных из модели 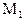соответствует гипотезе
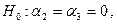
при которой модель 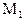редуцируется сразу к модели 
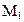. Критерий проверки гипотезы 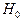основывается на статистике
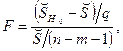
где 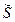– остаточная сумма квадратов в модели 
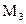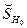, – остаточная сумма квадратов в модели , 
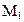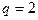– количество зануляемых параметров, 
.
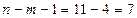Для наших данных получаем значение
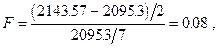
которое следует сравнить с критическим значением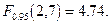 
Поскольку 
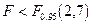, мы не отвергаем гипотезу 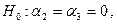и можем сразу перейти от модели 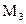к модели .
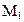Замечание. В рассмотренном примере мы действовали двумя способами:
Дважды использовали 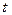-критерии, сначала приняв (не отвергнув) гипотезу 
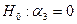в рамках модели 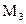, а затем приняв гипотезу 
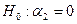в рамках модели 
.
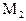Однократно использовали F- критерий, приняв гипотезу 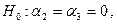в рамках модели .
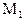Выводы при этих двух альтернативных подходах оказались одинаковыми. Однако, из выбора модели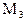 
в подобной последовательной процедуре, вообще говоря, не следует что такой же выбор будет обязательно сделан и при применении 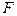-критерия, сравнивающего первую и последнюю модели.
