2015-05-18
1985
Рассмотрим возможные методы определения автокорреляции.
* Графический метод
Существует несколько вариантов графического определения автокорреляции. Один из них, указывающий отклонения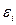 
с моментами t их получении (их порядковыми номерами i). Это так называемые последовательно-временные графики. В этом случае по оси абсцисс обычно откладывают либо время (момент) получения статистических данных, либо порядковый номер наблюдения, а по оси ординат- отклонения 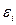(либо оценки отклонений 
)
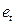* Метод рядов
Этот метод достаточно прост: последовательно определяются знаки отклонений 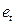,t=1,2…T. Например,
(-----)(+++++++)(---)(++++)(-),
Т.е. 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 наблюдениях.
Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.
Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция.
* Тест серий (Бреуша-Годфри)
Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении
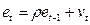, t =1,…,n (2.4.1)
(где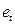 
-остатки регрессии, полученные обычным методом наименьших квадратов), коэффициент 
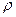окажется значимо отличающимся от нуля.
Практическое применение теста заключается в оценивании методом наименьших квадратов регрессии (2.4.1)
Преимущество теста Бреуша–Годфри по сравнению с тестом Дарбина-Уотсона содержит зону неопределенности для значений статистики d. Другим преимуществом теста является возможность обобщения: в число регрессоров могут быть включены не только остатки с лагом 1, но и с лагом 2,3 и т.д., что позволяет выявить корреляцию не только между соседними, но и между более отдаленными наблюдениями.
.
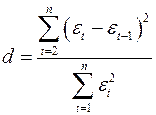Т.е. величина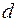 
есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Можно показать, что при больших значениях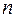 
существует следующее соотношение между критерием Дарбина-Уотсона 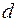и коэффициентом автокорреляции остатков первого порядка 
:
.
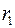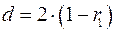Таким образом, если в остатках существует полная положительная автокорреляция и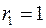 
, то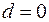 
. Если в остатках полная отрицательная автокорреляция, то 
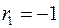и, следовательно, 
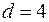. Если автокорреляция остатков отсутствует, то 
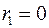и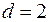 
. Т.е. 
.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза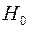 
об отсутствии автокорреляции остатков. Альтернативные гипотезы 
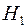и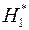 
состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона 
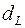и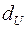 
для заданного числа наблюдений 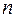, числа независимых переменных модели 
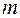и уровня значимости 
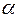. По этим значениям числовой промежуток 
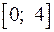разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью 
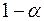осуществляется следующим образом:
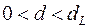– есть положительная автокорреляция остатков, 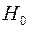отклоняется, с вероятностью 
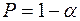принимается ;
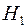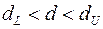– зона неопределенности;
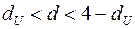– нет оснований отклонять 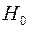, т.е. автокорреляция остатков отсутствует;
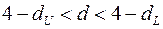– зона неопределенности;
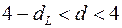– есть отрицательная автокорреляция остатков, 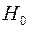отклоняется, с вероятностью 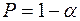принимается .
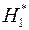Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу 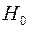Есть несколько существенных ограничений на применение критерия Дарбина–Уотсона. Во-первых, он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, т. е. к моделям авторегрессии. Во-вторых, методика расчета и использования критерия Дарбина – Уотсона направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорреляцию более высоких порядков следует применять другие методы. В-третьих, критерий Дарбина–Уотсона дает достоверные результаты только для больших выборок.
* Метод ранговой корреляции Спирмена
позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков.
Для подсчета ранговой корреляции Спирмена необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами значений могут быть:
1) два признака, измеренные в одной и той же группе испытуемых;
2) две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (например, личностные профили по 16-факторному опроснику Р. Б. Кеттелла, иерархии ценностей по методике Р. Рокича, последовательности предпочтений в выборе из нескольких альтернатив и др.);
3) две групповые иерархии признаков;
4) индивидуальная и групповая иерархии признаков.
Вначале показатели ранжируются отдельно по каждому из признаков. Как правило, меньшему значению признака начисляется меньший ранг.
