Пример 2.1. Данные о сменной добыче угля на одного рабочего (переменная Y – измеряется в тоннах), мощности пласта (переменная X 1 – измеряется в метрах) и уровнем механизации работ в шахте (переменная X 2 – измеряется в процентах), характеризующие процесс добычи угля в 10 шахтах приведены в таблице 2.1.
Предполагая, что между переменными Y, X 1, X 2 существует линейная зависимость, необходимо найти аналитическое выражение для этой зависимости, т.е. построить уравнение линейной регрессии.
Таблица 2.1
| Номер шахты i | xi 1 | xi 2 | yi |
Требуется определить:
1. Вычисление коэффициентов линейной множественной регрессии;
2. Вычисление коэффициентов линейной множественной регрессии и проверка значимости в режиме Регрессия;
3. Методические рекомендации по выполнению практических занятии
Цель работы. Используя пространственную выборку таблицы 3.1 необходимо вычислить вектор коэффициентов 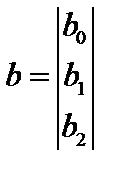
уравнения регрессии (3.1).
Расчетные соотношения. Вектор коэффициентов, найденный методом наименьших квадратов является решением следующей системы уравнений:
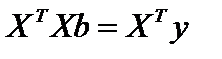 ,
,
где 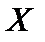 - матрица размера
- матрица размера 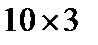 , первый столбец которой составлен из 1, а другие два столбца составлены из значений
, первый столбец которой составлен из 1, а другие два столбца составлены из значений 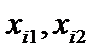 ,т.е. матрица
,т.е. матрица 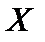 имеет следующую структуру (символы … означают не отображенные элементы)
имеет следующую структуру (символы … означают не отображенные элементы)
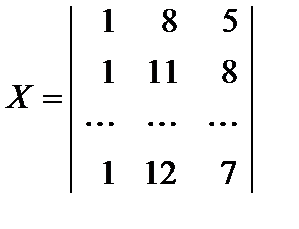 ,
,
а 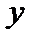 - вектор, составленный из 10 значений
- вектор, составленный из 10 значений 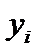 , т.е.
, т.е.
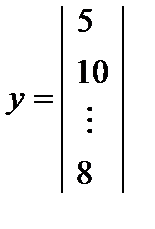 .
.
Матрица 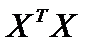 имеет обратную матрицу
имеет обратную матрицу 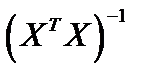 и тогда вектор коэффициентов вычисляется в виде:
и тогда вектор коэффициентов вычисляется в виде:
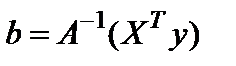 . (2.2)
. (2.2)
Матричные функции Excel. Для реализации этой матричной формулы в необходимо выполнить следующие операции: транспонирование; умножение матриц (частный случай – умножение матрицы на вектор); вычисление обратной матрицы. Все эти операции можно реализовать с помощью следующих матричных функций Exce l. Для работы с этими функциями можно или а) обратиться к Мастеру функций и выбрать нужную категорию функций, затем указать имя функции и задать соответствующие диапазоны ячеек, или б) ввести с клавиатуры имя функции задать соответствующие диапазоны ячеек.
Транспонирование матрицы осуществляется с помощью функции ТРАНСП (категория функций – Ссылки и массивы). Обращение к функции имеет вид:
ТРАНСП (диапазон ячеек),
где параметр диапазон ячеек задает все элементы транспонируемой матрицы (или вектора).
Умножение матриц осуществляется с помощью функции МУМНОЖ (категория функций – Математические).Обращение к функции имеет вид:
МУМНОЖ(диапазон_1;диапазон_2),
где параметр диапазон_1 задает элементы первой из перемножаемых матриц, а параметр диапазон_2 – элементы второй матрицы. При этом перемножаемые матрицы должны иметь соответствующие размеры (если первая матрица 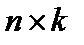 , вторая -
, вторая - 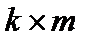 , то результатом будет матрица
, то результатом будет матрица 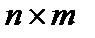 ).
).
Обращение матрицы (вычисление обратной матрицы) осуществляется с помощью функции МОБР (категория функций – Математические). Обращение к функции имеет вид:
МОБР (диапазон ячеек),
где параметр диапазон ячеек задает все элементы обращаемой матрицы, которая должна быть квадратной и невырожденной.
При использовании этих функций необходимо соблюдать следующий порядок действий:
· выделить фрагмент ячеек, в которые будет занесен результат выполнения матричных функций (при этом надо учитывать размеры исходных матриц);
· ввести арифметическое выражение, содержащее обращение к матричным функциям Excel;
· одновременно нажать клавиши [Ctrl], [Shift], [Enter]. Если этого не сделать, то вычислится только один элемент результирующей матрицы или вектора.
Решение. Сформируем матрицу 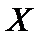 и вектор
и вектор 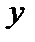 (см. рис. 2.1).
(см. рис. 2.1).
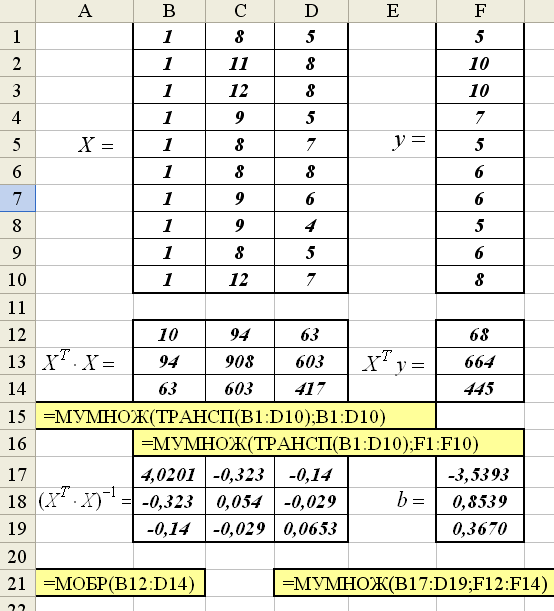
Рис. 2.1. Вычисление коэффициентов множественной регрессии
Затем выполним формирование матрицы 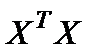 , вектора
, вектора 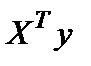 и вычисление вектора
и вычисление вектора 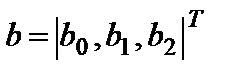 по формуле (3.2). Все эти вычисления показаны на рис. 2.1.
по формуле (3.2). Все эти вычисления показаны на рис. 2.1.
Получен вектор коэффициентов 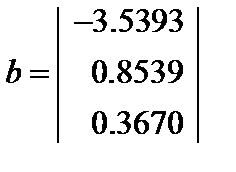 и тогда уравнение регрессии (2.1) примет вид:
и тогда уравнение регрессии (2.1) примет вид:
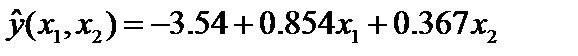 . (2.3)
. (2.3)
Цель работы. Используя пространственную выборку таблицы 2.1 и используя режим Регрессия необходимо вычислить вектор коэффициентов уравнения регрессии
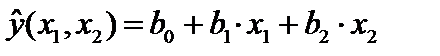 . (2.4)
. (2.4)
Режим Регрессия модуля Анализ данных. Табличный процессор Excel содержит модуль Анализ данных. Этотмодуль позволяет выполнить статистический анализ выборочных данных (построение гистограмм, вычисление числовых характеристик и т.д.). Режим работы Регрессия этого модуля осуществляет вычисление коэффициентов линейной множественной регрессии с 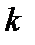 переменными, построение доверительные интервалы и проверку значимости уравнения регрессии.
переменными, построение доверительные интервалы и проверку значимости уравнения регрессии.
Для вызова режима Регрессия модуля Анализ данных необходимо:
· обратиться к пункту меню Сервис;
· в появившемся меню выполнить команду Анализ данных;
· в списке режимов работы модуля Анализ данных выбрать режим Регрессия и щелкнуть на кнопке Ok.
После вызова режима Регрессия на экране появляется диалоговое окно (см. рис. 2.2), в котором задаются следующие параметры:
1. Входной интервал Y – вводится диапазон адресов ячеек, содержащих значения 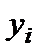 (ячейки должны составлять один столбец).
(ячейки должны составлять один столбец).
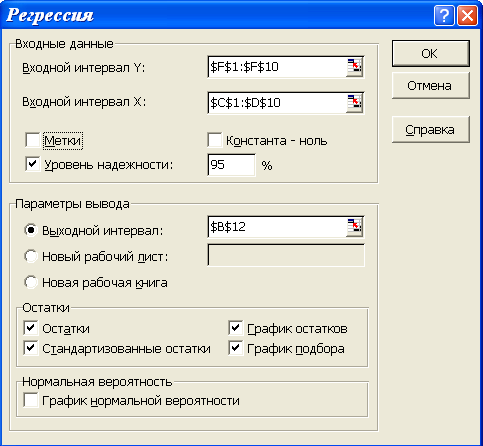
Рис. 3.2. Диалоговое окно режима Регрессия
2. Входной интервал X – вводится диапазон адресов ячеек, содержащих значения независимых переменных. Значения каждой переменной представляются одним столбцом. Количество переменных не более 16 (т.е. 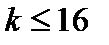 ).
).
3. Метки – включается если первая строка во входном диапазоне содержит заголовок. В этом случае автоматически будут созданы стандартные названия.
4. Уровень надежности – при включении этого параметра задается надежность 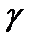 при построении доверительных интервалов.
при построении доверительных интервалов.
5. Константа-ноль – при включении этого параметра коэффициент 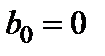 .
.
6. Выходной интервал – при включении активизируется поле, в которое необходимо ввести адрес левой верхней ячейки выходного диапазона, который содержит ячейки с результатами вычислений режима Регрессия.
7. Новый рабочий лист – при включении этого параметра открывается новый лист, в который начиная с ячейки А1 вставляются результаты работы режима Регрессия.
8. Новая рабочая книга - при включении этого параметра открывается новая книга на первом листе которой начиная с ячейки А1 вставляются результаты работы режима Регрессия.
9. Остатки – привключении вычисляется столбец, содержащий невязки 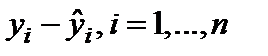 .
.
10. Стандартизованные остатки – при включении вычисляется столбец, содержащий стандартизованные остатки.
11. График остатков – при включении выводятся точечные графики невязки 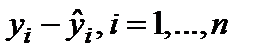 , в зависимости от значений переменных
, в зависимости от значений переменных 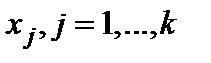 . Количество графиков равно числу
. Количество графиков равно числу 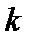 переменных
переменных 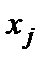 .
.
12. График подбора – при включении выводятся точечные графики предсказанных по построенной регрессии значений 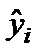 от значений переменных
от значений переменных 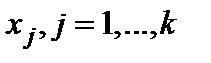 . Количество графиков равно числу
. Количество графиков равно числу 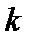 переменных
переменных 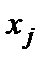 .
.
Решение. Первоначально введем в столбец С десять значений первой переменной, в столбец D - десять значений первой переменной (см. рис. 2.2), а в столбец F – десять значений зависимой переменной.
После этого вызовем режим Регрессия и в диалоговом окне зададим необходимые параметры (см. рис. 2.2). Результаты работы приводятся рис. 2.3 – 2.5. Заметим, из-за большой «ширины» таблиц, в которых выводятся результаты работы режима Регрессия, часть результатов помещены в другие ячейки.
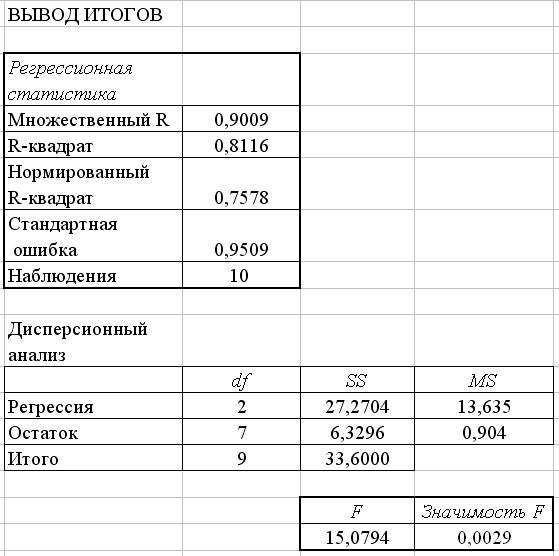
Рис. 2.3. Результаты работы режима Регрессия
Дадим краткую интерпретацию показателям, значения которых вычисляются в режиме Регрессия. Первоначально рассмотрим показатели, объединенные названием Регрессионная статистика (см. рис. 2.3).
Множественный 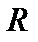 - корень квадратный из коэффициента детерминации.
- корень квадратный из коэффициента детерминации.
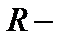 квадрат – коэффициент детерминации
квадрат – коэффициент детерминации 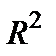 .
.
Нормированный 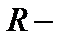 квадрат – приведенный коэффициент детерминации
квадрат – приведенный коэффициент детерминации 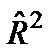 (см. формулу (2.1)).
(см. формулу (2.1)).
Стандартная ошибка – оценка 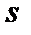 для среднеквадратического отклонения
для среднеквадратического отклонения  .
.
Наблюдения – число наблюдений 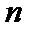 .
.
Перейдем к показателям, объединенных названием Дисперсионный анализ (см. рис. 2.3).
Столбец 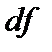 - число степеней свободы. Для строки Регрессия показатель равен числу независимых переменных
- число степеней свободы. Для строки Регрессия показатель равен числу независимых переменных 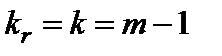 ; для строки Остаток - равен
; для строки Остаток - равен 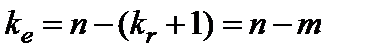 ; для строки Итого – равен
; для строки Итого – равен 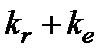 .
.
Столбец SS – сумма квадратов отклонений. Для строки Регрессия показатель равен величине 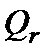 (см. формулы (1.16)), т.е.
(см. формулы (1.16)), т.е.
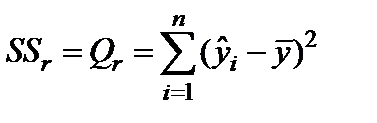 ;
;
для строки Остаток - равен величине 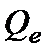 (см. формулы (1.16)), т.е.
(см. формулы (1.16)), т.е.
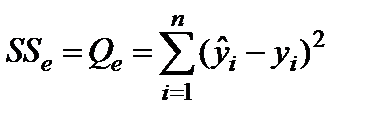 ;
;
для строки Итого – равен 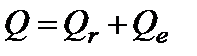 .
.
Столбец 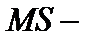 дисперсии, вычисленные по формуле
дисперсии, вычисленные по формуле
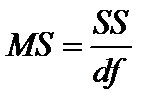 ,
,
т.е. дисперсия на одну степень свободы.
Столбец 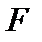 – значение
– значение 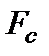 , равное
, равное 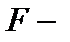 критерию Фишера, вычисленного по формуле:
критерию Фишера, вычисленного по формуле:
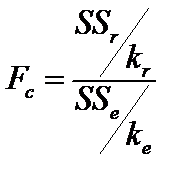 .
.
Столбец значимость 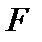 - значение уровня значимости, соответствующее вычисленной величине
- значение уровня значимости, соответствующее вычисленной величине 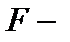 критерия и равное вероятности
критерия и равное вероятности 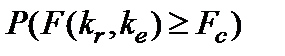 , где
, где 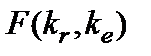 - случайная величина, подчиняющаяся распределению Фишера с
- случайная величина, подчиняющаяся распределению Фишера с 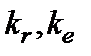 степенями свободы. Эту вероятность можно также определить с помощью функции FРАСП(
степенями свободы. Эту вероятность можно также определить с помощью функции FРАСП(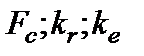 ). Если вероятность меньше уровня значимости
). Если вероятность меньше уровня значимости 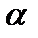 (обычно
(обычно 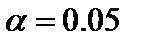 ), то построенная регрессия является значимой..
), то построенная регрессия является значимой..
Перейдем к следующей группе показателей, объединенных в таблице, показанной на рис. 2.4.
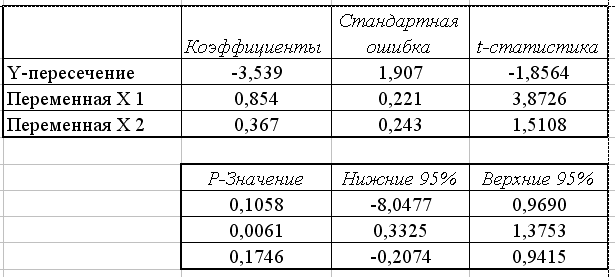
Рис. 2.4. Продолжение результатов работы режима Регрессия
Столбец Коэффициенты – вычисленные значения коэффициентов 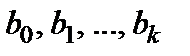 , расположенных сверху-вниз.
, расположенных сверху-вниз.
Столбец Стандартная ошибка – значения 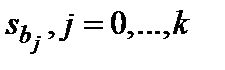 , вычисленные по формуле
, вычисленные по формуле 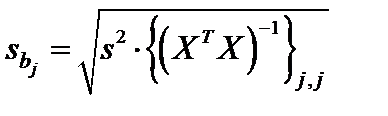 .
.
Столбец 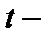 статистика – значения статистик
статистика – значения статистик 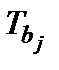 .
.
Столбец Р – значение – содержит вероятности случайных событий 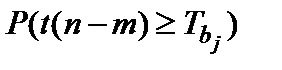 , где
, где 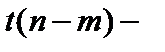 случайная величина, подчиняющаяся распределению Стьюдента с
случайная величина, подчиняющаяся распределению Стьюдента с 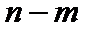 степенями свободы.
степенями свободы.
Если эта вероятность меньше уровня значимости 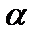 , то принимается гипотеза о значимости соответствующего коэффициента регрессии.
, то принимается гипотеза о значимости соответствующего коэффициента регрессии.
Из рис. 2.4 видно, что значимым коэффициентом является только коэффициент 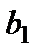 .
.
Столбцы Нижние 95% и Верхние 95% - соответственно нижние и верхние интервалы для оцениваемых коэффициентов 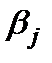 .
.
Перейдем к следующей группе показателей, объединенных в таблице, показанной на рис. 2.5.
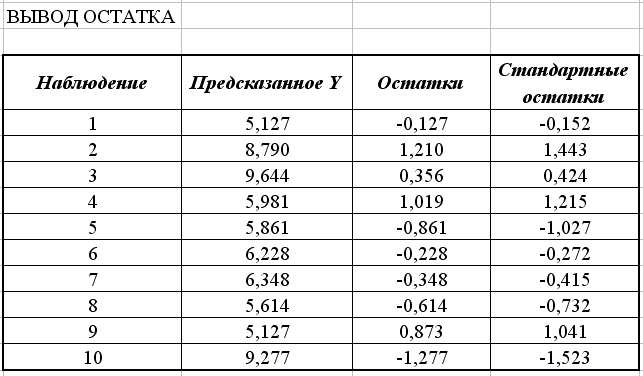
Рис. 2.5. Продолжение результатов работы режима Регрессия
Столбец Наблюдение – содержит номера наблюдений.
Столбец Предсказанное У – значения 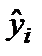 , вычисленные по построенному уравнению регрессии.
, вычисленные по построенному уравнению регрессии.
Столбец Остатки – значения невязок 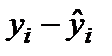
В заключении рассмотрения результатов работы режима Регрессия приведем график невязок (на рисунке 2.6 невязки названы остатками) 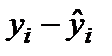 при заданных значениях только второй переменной. Наличие чередующихся положительных и отрицательных значений невязок является косвенным признаком отсутствия систематической ошибки (неучтенной независимой переменной) в построенном уравнении регрессии.
при заданных значениях только второй переменной. Наличие чередующихся положительных и отрицательных значений невязок является косвенным признаком отсутствия систематической ошибки (неучтенной независимой переменной) в построенном уравнении регрессии.
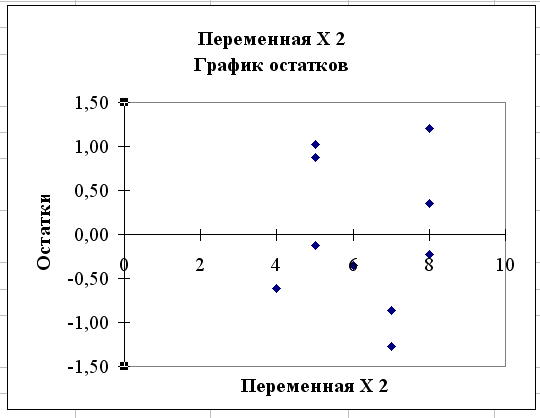
Рис. 2.6. График невязок как функция переменной 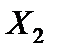
 2015-05-18
2015-05-18 1149
1149








