Построение степенной модели парной регрессии

Уравнение степенной модели имеет вид: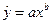

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: .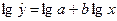

Обозначим 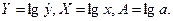Тогда уравнение примет вид: 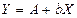, то есть получили линейное уравнение регрессии. Рассчитаем его параметры, используя МНК.

Составим рабочую таблицу.

N		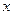X	у	Y	X2	XY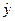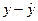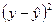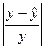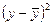
		1,000		1,415	1,000	1,415	10,008	15,992	255,733	0,615	11,56
		1,851		1,477	3,427	2,735	31,004	-1,004	1,008	0,033	54,76
		1,230		1,041	1,514	1,281	13,592	-2,592	6,721	0,236	134,56
		1,806		1,415	3,262	2,556	29,202	-3,202	10,253	0,123	11,56
		1,342		0,778	1,802	1,045	15,772	-9,772	95,495	1,629	275,56
		1,114		1,000	1,241	1,114	11,644	-1,644	2,702	0,164	158,76
		1,041		0,954	1,084	0,994	10,574	-1,574	2,478	0,175	184,96
		1,785		1,491	3,187	2,663	28,404	2,596	6,737	0,084	70,56
		1,919		1,643	3,683	3,154	33,927	10,073	101,475	0,229	457,96
		1,643		1,519	2,701	2,496	23,526	9,474	89,762	0,287	108,16
∑		14,73351		12,7342	22,9021	19,4510			572,364	3,575	1468,400

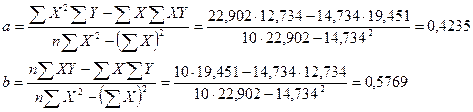
Уравнение регрессии имеет вид:

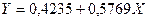
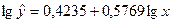
Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения.

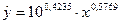
Получим уравнение степенной модели регрессии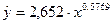

Так как в уравнении степенной регрессии параметр b совпадает с коэффициентом эластичности, то уравнение регрессии можно проинтерпретировать следующим образом: с увеличением объема капиталовложений на 1% объем выпуска продукции увеличивается в среднем на 0,58 %.

2) Определим индекс корреляции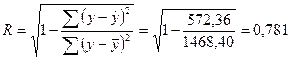

Связь между показателем у и фактором х можно считать достаточно сильной, так как R>0,7. Коэффициент детерминации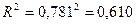

Вариация результативного признака у (объема выпуска продукции) на 61,0% объясняется вариацией фактора х (объема капиталовложений).

3) Рассчитаем F-критерий Фишера:

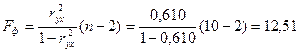
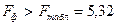для α=0,05; k₁=m=1, k₂=n-m-1=8.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как

Определим среднюю относительную ошибку аппроксимации:

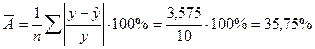
В среднем расчетные значения 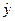для степенной модели отличаются от фактических значений на 35,75%, что выходит за пределы нормы.

Степенная модель не точная.